Introduction
In the previous article (see here) you saw how to create a class that best represents the graph model. In this article, you will see in detail some of its features such as the graph degree and the degree sequence.

Graph degree
Considering a graph, the degree of a node is the number of connections to the other nodes and is indicated by
deg(v)
You also need to consider cases where nodes can be connected to oneself. In this case the edge is called loop and the node in question will have two additional connections to consider in the node degree calculation.
As for the graph, the maximum degree of a graph, indicated by Δ(G), indicates the highest degree in its nodes, while the minimum degree of a graph, indicated by δ(G), indicates the smallest degree among the nodes of the graph.
To get a clear idea, consider the sample graph that was used in the previous article:
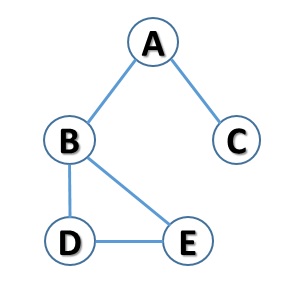
The maximum degree of the graph is equivalent to 3 (that of node B), while the minimum degree is 1 (that of node C). If I had an isolated node in the graph then the minimum grade would have been equal to 0.
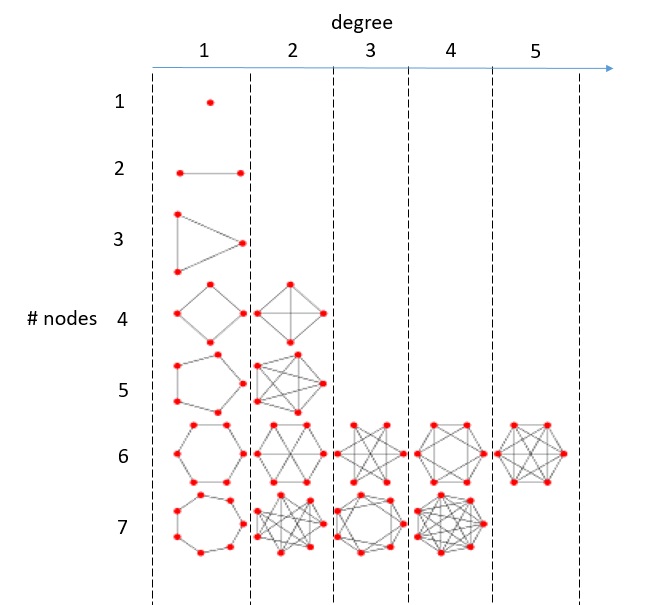
But consider a subclass of graphs: regular graphs. A graph is said to be regular when all its nodes have the same degree. Only then will you be able to talk about the degree of the graph. A regular graph with all k-nodes is called k-regular graph.
The following figure shows some regular graphs:
Handshaking Lemma
In order to continue with our analysis, ie in order to implement functions that can calculate the degrees of nodes and the degree of a graph we need to know a particular mathematical problem: handshaking lemma. This theorem states that in any non-oriented graph the nodes with an odd degree are in equal number. His particular name, “Handshaking,” is due to the fact that you can imagine an event in which a number of people must have exchanged the greeting with an odd number of other people’s hands.
This theorem is obtained from the degree sum formula:
∑v ∈ Vdeg(v) = 2 |E|
That is, the sum of the degrees of all nodes in the graph is equal to the number of E (edges) connections multiplied by two.
And from this it is concluded that the number of odd-numbered nodes must be equal. This conclusion is known just as handshaking lemma.
Calculation of degrees in a graph
Now that you have analyzed the necessary theory, move on to the implementation. First, write a function for calculating the degree of a node.
def node_degree(self, node):
adj_nodes = self.__graph[node]
degree = len(adj_nodes) + adj_nodes.count(node)
return degree
In calculating the degree of a node, you also need a function that controls the presence of isolated nodes within a graph.
def find_isolated_nodes(self):
graph = self.__graph
isolated = []
for node in graph:
print(isolated, node)
if not graph[node]:
isolated += [node]
return isolated
Now that you have basic functions, implement the delta() method that will allow you to calculate the minimum degree of a graph, and the Delta() method for the maximum degree of a graph.
def delta(self):
min = 100000000
for node in self.__graph:
node_degree = self.node_degree(node)
if node_degree < min:
min = node_degree
return min
def Delta(self):
max = 0
for node in self.__graph:
node_degree = self.node_degree(node)
if node_degree > max:
max = node_degree
return max
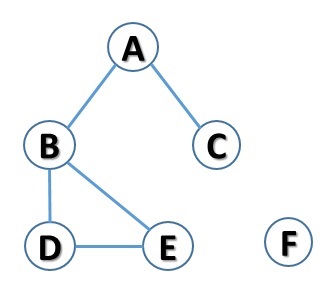
Try the newly written code, calculating the maximum degree and minimum degree of the sample graph. And check it by adding an isolated node, if the find_isolated_node() method manages to find it.
g = Graph(graph)
print("d(g): ", g.delta())
print("D(g): ", g.Delta())
g.add_node("F")
print(g.find_isolated_node())By running the code, you will get the following result:

The result is just what was expected.
Degree Sequence
Another very used feature in graph theory is the degree sequence of a graph. The sequence of degree of a non-oriented graph is defined as the sequence of degrees of its nodes in non-ascending order.
Again in this case you will implement a method that calculates the degree sequence of any graph.
def degree_sequence(self):
seq = []
for node in self.__graph:
seq.append(self.node_degree(node))
seq.sort(reverse=True)
return tuple(seq)
The method you just implemented returns a tuple containing the sequence sequence. Apply it to the sample graph
g = Graph(graph) print(g.degree_sequence())
Obtaining the following result:

Isomorphic Graphs
Any graph can exist in many forms, keeping the number of nodes and connections unchanged. So these shapes, actually appear as different graphs, called isomorphic graphs. So if you have two different graphs in analysis, it may often be useful to know if they are isomorphic (different shapes of the same graph)
The two graphs in the following figure are two isomorphic graphs.
Two graphs are isomorphic if:
- They have the same degree sequence
However, two graphs with the same degree sequence are not necessarily isomorphic.
The Erdös-Gallai’s Theorem
You’ve just seen how it’s possible to get a degree sequence from any graph. Now it would be interesting to know if, given a certain degree sequence, it is possible to draw a graph from it.
Erdös-Gallai’s theorem states that a non-increasing sequence of n numbers di (i = 1, …, n) is the degree sequence of a simple graph if and only if the sum of the sequence numbers is a pair number and if the following condition is met:

Then you will need to implement a method for this theorem that returns a boolean value, with true in case of positive and false in the negative. First, you will need to check if the sequence passed as argument is a degree sequence, checking that the sequence elements are not growing. For this control you will implement a separate function: is_degree_sequence(). Finally, the method will check that the inequalities of the theorem are met.
Define these methods as static methods, by adding the @staticmethod decorator, since these functions are related to the graphs but are not relevant and applicable to a single and specific instance.
@staticnethod
def is_degree_sequence(seq):
return all( x>=y for x, y in zip(seq, seq[1:]))
@staticmethod
def erdoes_gallai(dsequence):
if sum(dsequence) % 2:
return False
if Graph.is_degree_sequence(dsequence):
for k in range(1,len(dsequence) + 1):
left = sum(dsequence[:k])
right = k * (k-1) + sum([min(x,k) for x in dsequence[k:]])
if left > right:
return False
else:
return False
return True
Test this by first entering a degree sequence derived from the sample graph, and a sequence of invented values.
g = Graph(graph) s = g.degree_sequence() print(Graph.erdoes_gallai(s)) s2 = [4,3,3,2,2,1,1,1] print(Graph.erdoes_gallai(s))
By running the code you will get the following result.

Conclusions
In this article you have seen two other aspects in the theory of graphs: degree and degree sequence. In subsequent articles you will see more aspects of graph theory, and how many of these can be implemented with appropriate algorithms, further enriching the Graph class with additional functions.[:]