Gli scatterplots rappresentano un modo semplice di visualizzare la distribuzione di dati su di un piano XY, specialmente quando vogliamo evidenziare la presenza di clusters o di particolari andamenti. Ma quando si ha a che fare con insieme di dati composto da un enorme numero di campioni, molti di questi campioni si andranno sovrapponendo l’un l’altro durante la rappresentazione sul piano XY. Come vedremo nell’articolo, questo effetto di sovrapposizione dei campioni può rendere difficile l’analisi di eventuali cluster o andamenti di vario genere.

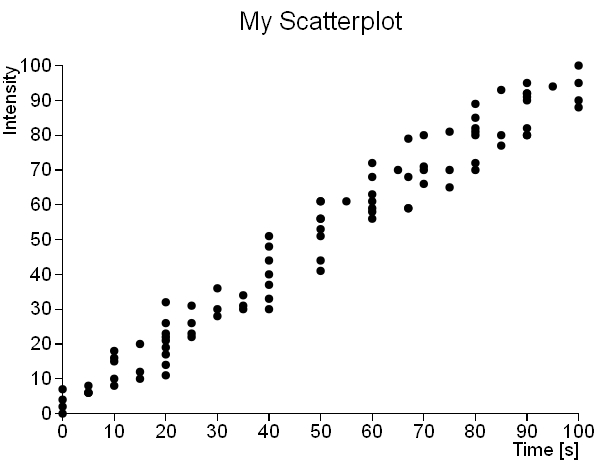
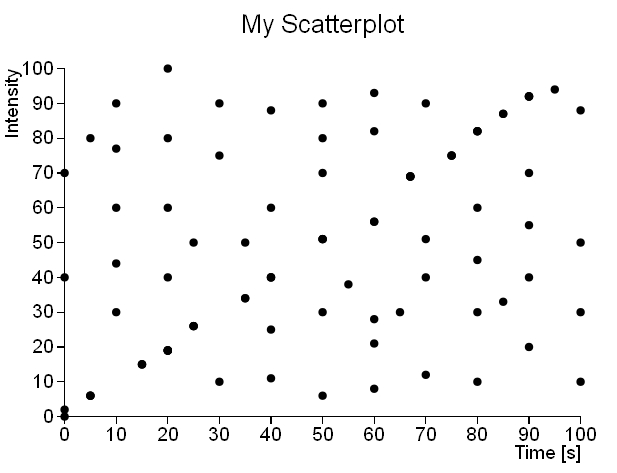
Prendiamo come esempio due diversi insiemi di dati e rappresentiamoli nei seguenti scatterplot (Fig 1 e 2). Il primo scatterplot (vedi Fig.1) mostra senza alcun equivoco che l’insieme di dati segue un andamento lineare. Invece il secondo insieme di dati mostra uno scatterplot (vedi Fig.2) in cui i punti sono uniformemente distribuiti per tutto il piano XY (apparentemente, in realtà non è così.
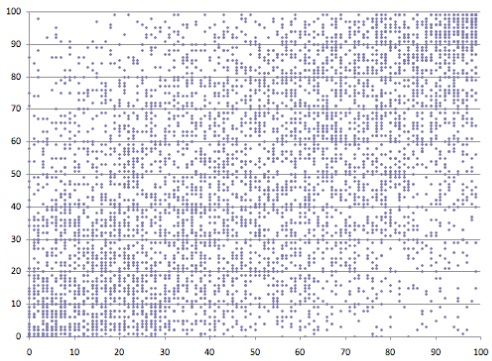
Nota: Ho utilizzato questo semplice dataset con pochi campioni per rendere più semplice la comprensione dei concetti che sono alla base di questo articolo. La figura seguente (Fig.3) mostra invece un caso reale.
Se analizziamo numericamente il secondo insieme di dati, invece di considerare lo scatterplot, possiamo notare che molti punti occupano lo stesso posto nel piano XY. Quindi in uno scatterplot appariranno come un singolo punto, celando così in un certo modo la reale distribuzione dei punti. Quindi solo fino ad un certo punto uno scatterplot può rappresentare la densità di una distribuzione di dati.
In questi casi, abbiamo bisogno di scegliere un’altra tipologia di rappresentazione grafica. Una visualizzazione che faccia uso dei metodi di binning, al fine di visualizzare la densità dei punti nel piano XY anzichè i punti stessi. Il binning è una tecnica di aggregazione dei dati che è in grado di rilevare schemi che normalmente possono non apparire all’interno di uno scatterplot.
Binning
Il Binning è una tecnica di aggregazione di dati utilizzata per raggruppare un insieme di N dati in un numero minore di gruppi di dati. In questo articolo considereremo solo il caso di insiemi costituiti da dati (x,y) cioè distribuibili in un piano XY. Ma questa tecnica è applicabile in tantissimi altri casi.
I concetti che stanno alla base del binning sono piuttosto semplici e possono essere elencati quanto segue:
- il piano XY viene suddiviso uniformemente in diversi poligoni regolari (quadrati, triangoli o esagoni).
- si conta il numero dei punti contenuti in ciascuna cella (bin) che viene riportato in una struttura dati.
- le celle che presentano un conteggio > 0 vengono rappresentate usando una scala di colori (heatmap) o con differenti dimensioni in rapporto al valore riportato dal conteggio stesso.
Nota: se consideriamo il caso di un insieme di dati monodimensionali, la tecnica di binning produce un semplice istogramma.
Il Binning Rettangolare
Il metodo più semplice di binning fa uso di celle quadrate, e per la maggior parte degli scopi questo tipo di suddivisione può essere sufficiente, sfruttandone così la semplicità computazionale.
Se sei interessato maggiormente all’argomento c’è un articolo (tutorial) in cui viene realizzato un binning rettangolare utilizzando la libreria JavaScript D3.
Il Binning Esagonale
Questa tecnica è stata descritta la prima volta nel 1987 (D.B.Carr et al. Scatterplot Matrix Techniques for large N, Journal of the American Statistical Association, No.389 pp 424-436). Ci sono parecchie ragioni per utilizzare il binning esagonale al posto di quello rettangolare quando si ha una superficie 2D come il piano XY. La più evidente è che l’esagono è più simile al cerchio del quadrato. Ciò si traduce in una più efficiente forma di aggregazione dei dati rispetto al centro di una cella (bin) da parte degli esagoni rispetto ai quadrati. Tutto questo può essere evidenziato ulteriormente andando a vedere alcune proprietà degli esagoni e, particolarmente, della tassellazione esagonale.
- L’esagono è il poligono con il maggiore numero di lati che sia in grado di formare una tassellazione regolare di un piano 2D.
Ciò rende il binning esagonale il metodo più efficiente e compatto di suddivisione di uno spazio 2D.
Infatti, sebbene sia possibile creare molti schemi di tassellazione utilizzando combinazioni di due o più tipologie di poligoni, ciò non è possibile quando si vuole utilizzare un solo tipo di poligono regolare, eccetto per i quadrati, i triangoli e gli esagoni.
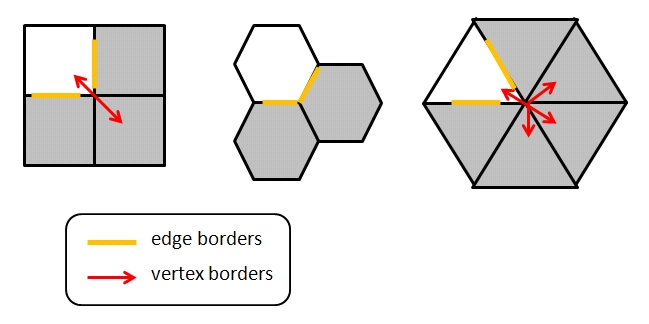
- In un binning esagonale un esagono condivide un lato per ciascun esagono adiacente.
Invece in un binning di quadrati e trangoli, alcune bin adiacenti condividono solo un vertice e non un lato (vedi FIg.7).
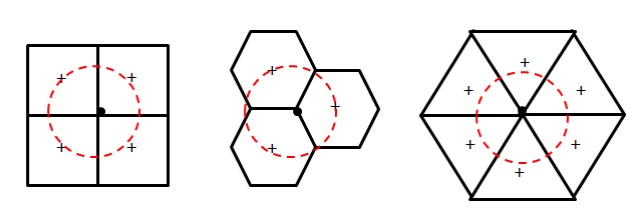
Considerando poligoni aventi tutti la stessa area, più il poligono sarà simile ad un cerchio, più vicini al suo centro risulteranno i punti ai bordi (specialmente ai vertici).
Quindi ciascun punto all’interno di un esagono è probabilmente più vicino al centro rispetto a quanto potrebbe essere in un quadrato o in un triangolo. Ciò è dovuto al fatto che triangoli e quadrati hanno angoli più acuti rispetto agli esagoni.
Gli Scatterplot “sparsi” e il Binning esagonale
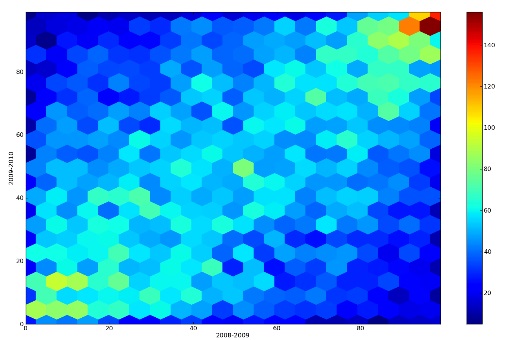
Ora che abbiamo un’idea di che cosa sia un binning esagonale, sottoponiamo lo stesso dataset che aveva generato lo scatterplot “sparso” al binning esagonale. Quello che segue (vedi Fig.9), ne è il risultato:
Ho utilizzato un intervallo di colori che va dal giallo al rosso scuro. Le celle bianche indicano i punti in cui non è presente alcun dato campione (count = 0). Come possiamo vedere in Fig.8, ora un andamento lineare è ben visibile (la traccia rossa).
Binning esagonale multivariato
Questo effetto può essere ulteriormente accentuato se consideriamo l’eventualità di disegnare gli esagoni con diverse dimensioni a seconda del valore del conteggio. Il risultato di tale approccio è visibile nella figura seguente (Fig.10). In questo caso la variabile rappresentata dalla scala di colori e dalle dimensioni degli esagoni è la stessa. Ma generalmente possono differire, cioè la dimensione degli esagoni potrebbe esprimere il valore della deviazione standard per ciascuna bin. In questo caso abbiamo un binning multivariato (a più variabili).
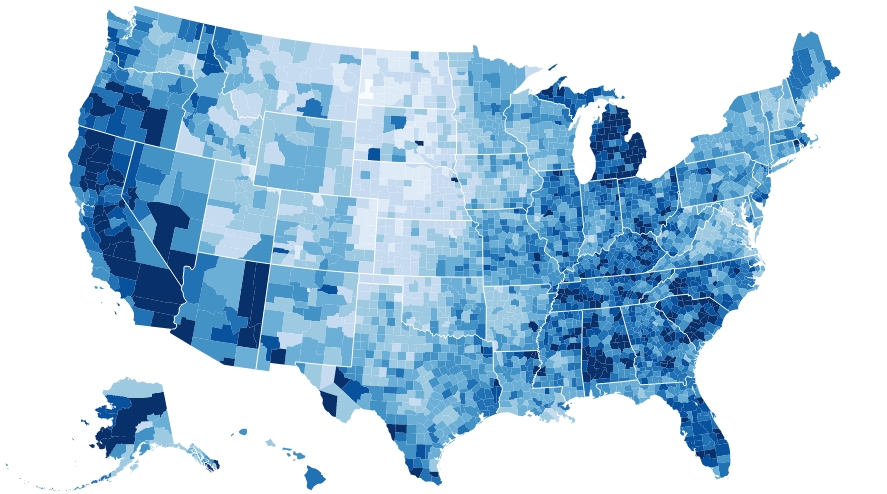
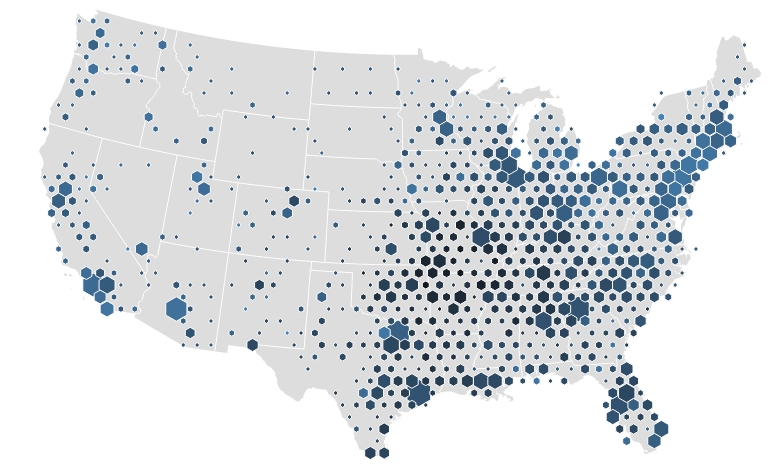
Le mappe coropletiche
Proprio in questi ultimi mesi, il binning esagonale sta avendo una rapida diffusione in un campo specifico: la cartografia. Infatti questo argomento sta diventando assai popolare in molti articoli e post su blog nei quali vengono illustrate le sue diverse applicazioni: soprattutto nella generazione delle mappe coropletiche.
Le mappe coropletiche sono delle mappe tematiche in cui le aree sono colorate o rappresentate con diversi schemi che evidenziano i risultati di calcoli statistici effettuate su di esse.
La novità sta proprio nell’utilizzo del binning esagonale per rappresentare dati statistici nelle mappe. Questo approccio può essere un metodo molto efficace di gestire enormi moli di dati e rappresentarli in modo molto semplice ed intuitivo nelle mappe.
References
- C. Stucchio – Don’t use scatterplots
- N. Lewin-Koh – Hexagon Binning: an Overview.
- Hexbins!
- Graham – An introduction to Hexagonal Geometry
Choropleth Maps with D3
- S.Hall – Delimited – Hexbins with D3 and Leaflet Maps
- M. Bostock – Choropleth
- M. Bostock – Bivariate Hexbin Map