OpenCV & Python - Analisi dei contorni e dei gradienti di un'immagine

Post Views: 54.431

Introduzione

In questo articolo, appartenente alla serie OpenCV utilizzando Python, parleremo dell’analisi dei contorni e dei gradienti di una immagine. Vedremo come grazie all’applicazione di alcuni filtri sarà possibile evidenziare l’andamento del gradiente di colore ed in particolare rilevare i contorni o i bordi di un’immagine.

La teoria dei Gradienti di immagini

Tra le varie operazioni che si possono applicare a delle immagini, esistono le convoluzioni di una immagine in cui si applicano dei filtri che modificano in qualche modo l’immagine. Abbiamo già visto che un’immagine viene rappresentata come una grossa matrice numerica in cui i colori di ogni singolo pixel dell’immagine viene rappresentato da un numero da 0 a 255 all’interno della matrice. Le convoluzioni non fanno altro che elaborare tutti questi valori numerici, applicando una operazione matematica (filtro immagine) per produrre nuovi valori all’interno di una nuova matrice della stessa dimensione.

Una di queste operazioni è appunto la derivata. In parole semplici la derivata è un’operazione matematica che ci permette di ottenere dei valori numerici che indicano la rapidità con cui un valore varia (nello spazio, nel tempo, ecc..).

Come potrebbe essere importante la derivata nel caso delle immagini? A noi interessa la variazione di colore chiamato gradiente.

Il poter calcolare il gradiente di un colore è un ottimo strumento per calcolare i bordi di un’immagine. Infatti il nostro occhio riesce a distinguere i contorni di una figura presente in un’immagine proprio grazie ai salti tra un colore in un altro. Inoltre il nostro occhio è in grado di percepire le profondità proprio grazie alle varie sfumature di colore che vanno dal chiaro allo scuro, appunto il gradiente.

Da tutto ciò risulta ben chiaro quanto può essere importante poter in qualche modo misurare il gradiente presente in una immagine e rilevare anche i bordi delle figure con una semplice operazione (filtro) effettuata su una immagine.

Per vedere meglio la cosa dal punto di vista matematico facciamo un esempio.

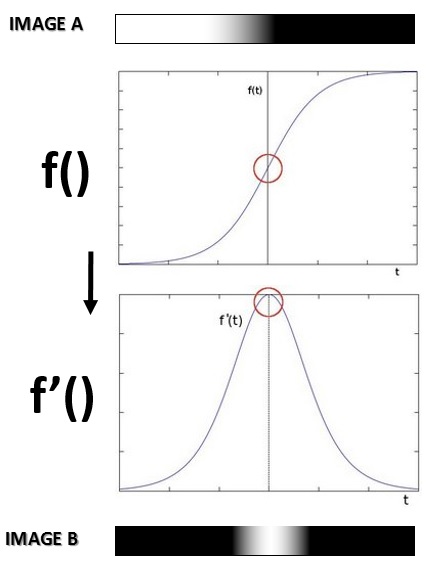
Come puoi ben vedere dalla figura, un bordo (edge) o contorno in un’immagine non è altro che un breve passaggio da una tonalità ad un altra di un colore. Per semplificare, lo 0 è il nero e 1 è il bianco. Tutti i valori intermedi di grigio saranno compresi tra 0 e 1.

Se mettiamo tutti i valori corrispondenti al gradiente in un grafico otteniamo la funzione f(). Come possiamo vedere in corrispondenza del bordo abbiamo un repentino passaggio da 0 ad 1.

Calcoliamo la derivata della funzione f() e otteniamo la funzione f'(). Come possiamo vedere, dove abbiamo la massima variazione di tonalità avremo valori prossimi ad 1. Quindi riconvertendo in colore, otterremo una figura in cui il colore bianco indicherà il bordo (edge) o contorno della figura.

Il calcolo della derivata – La derivata di Sobal e il Laplaciano

Per chi è interessato a come viene calcolata la derivata di una matrice può leggere questo paragrafo, altrimenti può passare direttamente al caso pratico più avanti.

La derivata di una matrice viene calcolata tramite un operatore chiamato Laplaciano, in onore di Laplace, un famoso matematico.

$\Delta src = \frac{\partial ^2{src}}{\partial x^2} + \frac{\partial ^2{src}}{\partial y^2}$

Purtroppo, come sappiamo bene per chi lavora con i computer, le derivate parziali non possono essere risolte analiticamente ma devono essere trattate con il calcolo numerico tramite delle approssimazioni. Quindi per ottenere un Laplaciano abbiamo bisogno di calcolarci prima due derivate, chiamate derivate di Sobal, ognuna delle quali tiene conto delle variazioni di gradiente in una determinata direzione: una orizzontale, l’altra verticale.

Derivata orizzontale di Sobal (Sobal x). Si ottiene attraverso la convoluzione * dell’immagine I con una matrice $G_{x}$ chiamata kernel sempre di dimensioni dispari. Il caso più semplice, quello con kernel di dimensione 3 è il caso seguente:

$G_{x} = \begin{bmatrix} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{bmatrix} * I$

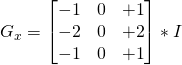
Derivata verticale di Sobal (Sobal y). Si ottiene attraverso la convoluzione * dell’immagine I con una matrice $G_{y}$ chiamata kernel, sempre di dimensioni dispari. Il caso più semplice, quello con kernel di dimensione 3 è il caso seguente:

$G_{y} = \begin{bmatrix} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{bmatrix} * I$

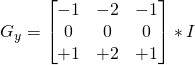
Quindi alla fine per ottenere il Laplaciano (un’approssimazione) si combinano i due risultati precedenti

$G = \sqrt{ G_{x}^{2} + G_{y}^{2} }$

anche se a volte si preferisce semplificare anche questa equazione utilizzzando

$G = |G_{x}| + |G_{y}|$

Più è bassa la dimensione del kernel, maggiore sarà l’approssimazione con cui otterremo i risultati. Però al tempo stesso al crescere delle dimensioni del kernel maggiori saranno le richieste di calcolo. Per un kernel di dimensione 3 comunque l’approssimazione può essere davvero eccessiva, ed è meglio utilizzare la funzione di Scharr (anch’essa disponibile in OpenCV). Per quanto riguarda gli esempi in questo articolo utilizzeremo un kernel di dimensione 5 che è un buon compromesso calcolo-approssimazione.

$G_{x} = \begin{bmatrix} -3 & 0 & +3 \\ -10 & 0 & +10 \\ -3 & 0 & +3 \end{bmatrix} G_{y} = \begin{bmatrix} -3 & -10 & -3 \\ 0 & 0 & 0 \\ +3 & +10 & +3 \end{bmatrix}$

Prima di cominciare

Per prima cosa per eseguire il codice presente in questo articolo sono necessari alcuni prerequisiti.

Far partire l’ambiente virtuale su cui avete compilato ed installato la libreria OpenCV.

source ~/.profile
workon cv
(cv) $

Se non aveste ancora installato OpenCV, seguite la procedura di installazione descritta in questo articolo.

Inoltre in questo esempio per migliorare la visualizzazione di più immagini contemporaneamente, sfrutteremo la libreria grafica matplotlib. Se ancora non l’avete installata sul vostro ambiente virtuale potete farlo scrivendo

pip --no-cache-dir install matplotlib

poi installate il pacchetto TKinter necessario per il corretto funzionamento di matplotlib.

sudo apt-get install python-tk

Infine scaricate l’immagine di prova che servirà per vedere bene l’effetto di rilevamento dei bordi in un sistema in bianco e nero. Salvatela come blackandwhite.jpg.

Poi utilizzeremo un’immagine contenente dei gradienti, scaricatela e salvatela come gradient.jpg.

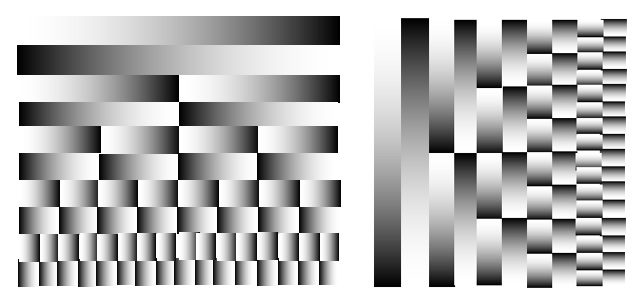
Inoltre alla fine faremo qualche prova anche su un’immagine a colori e ricca di bordi e di gradienti di colore. Scaricate l’immagine seguente (se non l’avete già fatto negli esempi precedenti) e salvatela come logos.jpg.

Rilevazione dei bordi

Scrivete quindi il codice seguente per il caso pratico.

import cv2
import numpy as np
from matplotlib import pyplot as plt

img = cv2.imread('blackandwhite.jpg',0)

laplacian = cv2.Laplacian(img, cv2.CV_64F)
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5)
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=5)

plt.subplot(2,2,1),plt.imshow(img,cmap = 'gray')
plt.title('Original'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,2),plt.imshow(laplacian,cmap = 'gray')
plt.title('Laplacian'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,3),plt.imshow(sobelx,cmap = 'gray')
plt.title('Sobel X'), plt.xticks([]), plt.yticks([])
plt.subplot(2,2,4),plt.imshow(sobely,cmap = 'gray')
plt.title('Sobel Y'), plt.xticks([]), plt.yticks([])

plt.show()

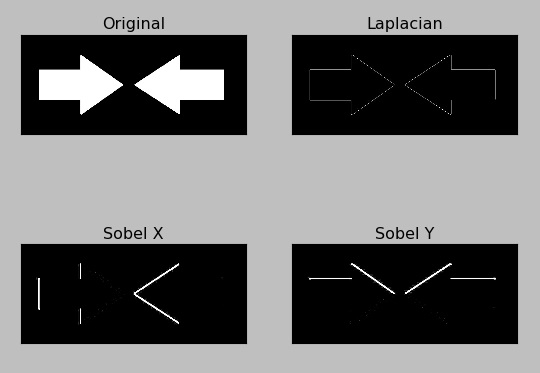
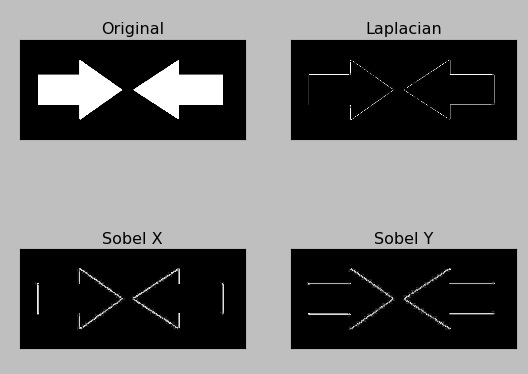
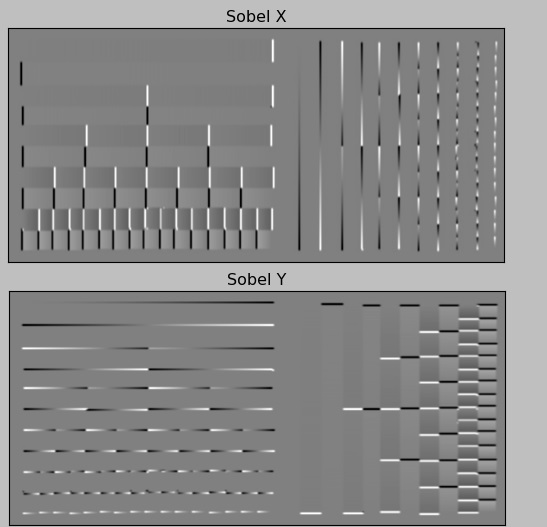
Eseguendo il codice si ottiene l’immagine seguente con i 4 riquadri in cui il primo in alto a sinistra è l’immagine in bianco e nero originale, mentre gli altri tre sono il risultato dei tre filtri applicati all’immagine.

Per quanto riguarda i filtri di Sobel, il rilevamento dei bordi è perfetto solo che limitato o orizzontalmente o verticalmente. Le linee diagonali sono visibili in entrambe i casi dato che hanno componenti sia orizzontali che verticali, ma i bordi orizzontali nel Sobel X e quelli verticali nel Sobel Y non vengono rilevati in alcun modo.

Combinando i due filtri (il calcolo delle due derivate) per dare il filtro Laplaciano, la determinazione dei bordi è omnidirezionale ma si ha una certa perdita di risolutezza. Infatti si possono vedere che i ‘rilievi’ corrispondenti ai bordi sono più tenui.

La colorazione in grigio è molto utile per rilevare sia i bordi che i gradienti, ma se siamo interessati a rilevare esclusivamente i bordi, dobbiamo ottenere come output un file immagine in cv2.CV_8U.

Quindi potremmo sostituire il tipo di data in uscita da cv2.CV_64F in cv2.CV_8U nei tre filtri del codice precedente,

laplacian = cv2.Laplacian(img, cv2.CV_8U)
sobelx = cv2.Sobel(img,cv2.CV_8U,1,0,ksize=5)
sobely = cv2.Sobel(img,cv2.CV_8U,0,1,ksize=5)

ed eseguendo il codice ottenere i risultati in bianco e nero, dove con i bianchi vengono visualizzati i bordi delle figure presenti nell’imagine.

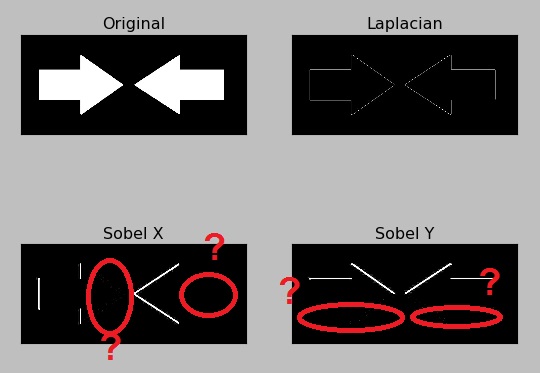
Ma se osservate bene i riquadri del filtro Sobel X e Y noterete subito che qualcosa è andato storto. Dove sono andati a finire alcuni bordi?

In effetti si è verificato un problema durante la conversione dei dati. I gradienti segnalati nella scala dei grigi con valori cv2.CV_64F sono rappresentati da valori positivi (pendenza positiva) quando si passa da nero a bianco mentre da valori negativi (pendenza negativa) quando si passa da bianco a nero. Nella conversione da cv2.CV_64F a cv2.CV_8U, tutte le pendenze negative vengono ridotte a 0 e quindi le informazioni relative a quei bordi vengono perse. Quando si andrà a rappresentare l’immagine i bordi che delimitano zone di gradiente da bianco a nero non verranno rappresentate.

Per ovviare a questo si deve mantenere il dato in uscita del filto in cv2.CV_64F (invece che cv2.CV_8U), calcolarsi poi il valore assoluto ed infine fare la conversione in cv2.CV_8U.

laplacian64 = cv2.Laplacian(img, cv2.CV_64F)
sobelx64 = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=5)
sobely64 = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=5)

laplacian = np.uint8(np.absolute(laplacian64))
sobelx = np.uint8(np.absolute(sobelx64))
sobely = np.uint8(np.absolute(sobely64))

Ed eseguendo ottenere la giusta rappresentazione in bianco su nero dei bordi delle figure.

Adesso si notano bene i bordi che non vengono visualizzati in Sobel X e sobel Y perchè paralleli alla direzione di rilevamento (orizzontale e verticale).

Osserviamo i gradienti

Abbiamo visto che l’applicazione dei filtri Laplaciano e Sobel sono in grado di fornirci oltre che i bordi anche il livello di gradienti attraverso una scala di grigi. Applichiamo quello che abbiamo visto con l’immagine gradient.jpg.

Quindi si vede bene in figura come l’assenza di gradiente venga rappresentata da un grigio intermedio, mentre al crescere della velocità del gradiente nel passare dal bianco la figura utilizzi come indicatore un grigio sempre più scuro, mentre l’inverso, dal nero al bianco, la figura utilizzi un grigio sempre più chiaro. Fino ad arrivare in entrambe i casi ai bordi (salto da bianco a nero, e viceversa) indicati con nero e bianco rispettivamente.

Se infine applichiamo quello che abbiamo visto ad un’immagine reale ricca di colori e bordi come per esempio logos.jpg, otterremo la figura seguente:

Conclusione

Abbiamo visto in questo articolo come la libreria OpenCV ci offre una serie di strumenti per l’analisi dei gradienti presenti in un’immagine applicando dei filtri alle immagini stesse. In altri articoli della serie OpenCV potrai approfondire l’argomento o vedere altri casi molto interessanti per l’analisi delle immagini.

OpenCV & Python – Analisi dei contorni e dei gradienti di un’immagine