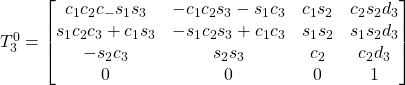Forward Kinematics
Forward kinematics allows us to determine the position and orientation of the end-effector in terms of the joint variables. A simple way to explain direct kinematics is to take a very simple case and apply the basic methodologies of this technique to it.

The manipulator with 2 links and 2 joints
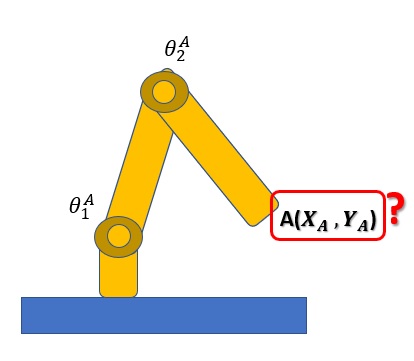
A very simple case of robotics with which to apply direct kinematics is the 2-link and 2-joint manipulator. Now the classic problem of direct kinematics will be that, given the length of links l1 and l2, and the angles assumed by the two joints θ1 and θ2,, to derive the position of the effective end with the coordinates x and y.
In practical cases, manipulators often have internal sensors that allow to know in real time the position or angle of the various joints. Therefore we will take for granted the knowledge of the values of the two angles θ1 and θ2 which will be used as base values for our calculations.
The first thing to do will be to establish a fixed coordinate system, called the base frame. In the case of manipulators, the base of the manipulator (opposite end to the effective end) is referred to as the basis of the coordinates O0x0y0.
The (x, y) coordinates of the tool are expressed as:
![]()
![]()
Where l1 and l2 are the lengths of the two links. The orientation of the tool frame relative to the base frame is also given by the direction of the cosines of the x2 and y2 axes with respect to the x0 and y0 axes.
![]()
![]()
![]()
![]()
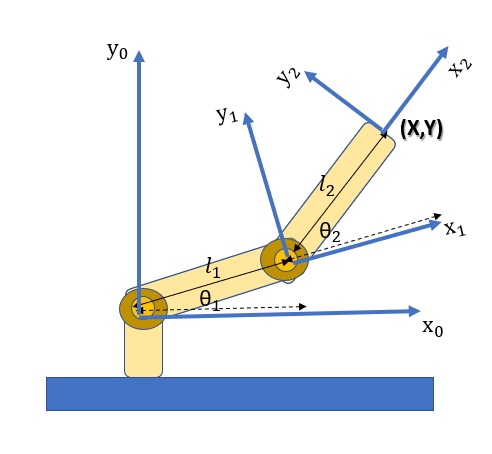
These four equations can be combined to obtain an orientation matrix.
![]()
The equations we have just defined are called the forward kinematic equations and sno specific to the manipulator under consideration.
More complex cases – the Denavit-Hartenberg procedure
The case of the 2-link and 2-joint manipulator is a basic example, but other more advanced cases can lead to equations that are too complex and often not easily writable.
In any case, there is a general procedure that allows you to establish a coordinate system for each joint, and then to pass from one system to another through matrix transformations. This procedure is called the Denavit-Hartenberg procedure.
In this procedure, homogeneous coordinates and homogeneous transformations will be used to simplify the transformation between the different coordinate systems
There are therefore conventions, called Denavit-Hartenberg conventions.
The numbering of links and joints
The links are numbered from 0 to n starting from the base and arriving at the effective end, and are indicated with ![]() . This describes a serial manipulator with a chain of n + 1 links. This manipulator will consequently have n joints, which will be indicated in turn with
. This describes a serial manipulator with a chain of n + 1 links. This manipulator will consequently have n joints, which will be indicated in turn with ![]() .
.
The link ![]() will be the one that connects the joint
will be the one that connects the joint ![]() with the one
with the one ![]() .
.
Assignment of the z axes of the different reference systems (frames)
Each link ![]() is associated with a frame of integral coordinates
is associated with a frame of integral coordinates ![]() whose axis
whose axis ![]() coincides with l ‘axis of the joint
coincides with l ‘axis of the joint ![]() , ie of the joint downstream in the chain (the one closest to the effective end). Since the joints generally rotate on a plane, z is indicated as the axis perpendicular to this plane.
, ie of the joint downstream in the chain (the one closest to the effective end). Since the joints generally rotate on a plane, z is indicated as the axis perpendicular to this plane.
The basic element: link-joint
Therefore the Denavit-Hartenberg procedure mainly consists of considering as the basic element of a manipulator, a pair of joints with the link that joins them. Each base element thus defined will correspond to a coordinate transformation matrix

There are therefore two joints ![]() and
and ![]() and the link
and the link ![]() interposed, with the two reference systems defined together
interposed, with the two reference systems defined together ![]() and
and ![]() .
.
In choosing the reference systems, proceed as follows:
- the axis
 is chosen coincident with the axis of the joint
is chosen coincident with the axis of the joint 
- the axis
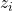 coinciding with the axis of the joint
coinciding with the axis of the joint 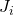 ;
; - the
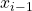 axis can be freely chosen, but it is convenient to place it in the direction of the next joint, and it intersects with
axis can be freely chosen, but it is convenient to place it in the direction of the next joint, and it intersects with  in correspondence of the center of the joint
in correspondence of the center of the joint 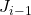 (chosen as origin);
(chosen as origin); - the
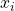 axis runs along the common normal between the
axis runs along the common normal between the  and
and 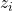 axes;
axes; - the axes
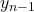 and
and 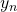 are chosen in order to complete the respective left-handed triples.
are chosen in order to complete the respective left-handed triples.
The transformation is then described by four Denavit-Hartenberg parameters:
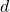 which is the distance of the
which is the distance of the  axis from the common normal; in case there are infinite common normals (axes
axis from the common normal; in case there are infinite common normals (axes 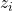 e and
e and  parallel) the value of
parallel) the value of 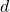 will be chosen more convenient;
will be chosen more convenient;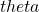 is the angle of rotation around the
is the angle of rotation around the  axis needed to align
axis needed to align 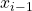 with [ latex] x_i [/latex];
with [ latex] x_i [/latex]; (sometimes also referred to as
(sometimes also referred to as  is the minimum distance between the axes
is the minimum distance between the axes  and
and 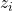 ;
;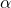 is the angle of rotation around the common normal (ie around
is the angle of rotation around the common normal (ie around 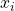 ) to align the
) to align the  axis to
axis to 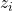 .
.
It can be seen that the ![]() axis is perpendicular to both the
axis is perpendicular to both the ![]() axis and the
axis and the ![]() axis and intersects both.
axis and intersects both.
Coordinate transformation
Each arm-joint pair can be described as a coordinate transformation operation between the two reference systems associated with the joints.
If you choose to orient the ![]() axis along the common normal between the
axis along the common normal between the ![]() and
and ![]() axes, the transformation matrix is defined as a series of two consecutive rototranslations:
axes, the transformation matrix is defined as a series of two consecutive rototranslations:
![]()
Where



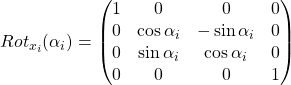
From here we obtain the complete transformation matrix:
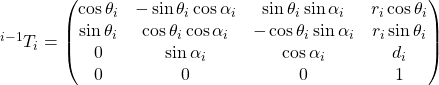
Now that we know the coordinate transformation matrix for each single link-joint base element, it is possible to apply direct dynamics on any type of chain manipulator. It is sufficient to break down the manipulator, however complex, into its basic elements, calculate the transformation matrices for each element, and then multiply them to obtain a general matrix.
Let’s see some examples of more complex manipulators.
Three-arm planar manipulator
The three-arm manipulator is made up of three basic elements, whose joints all rotate on the same plane.
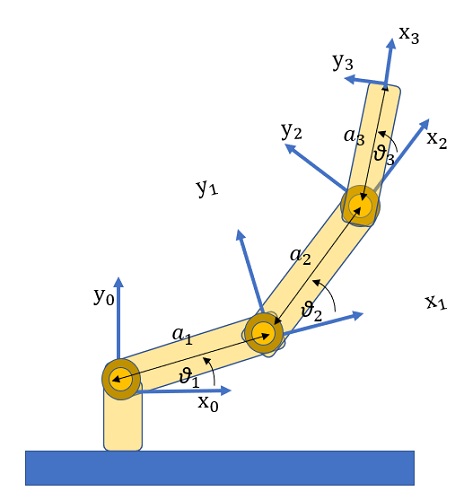
First, then, the four Denavit-Hartenberg parameters are defined for each base element and reported in a table.
| BASE Element | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
From the basic elements table it can be seen that the transformation matrices will be identical:
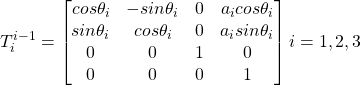
and therefore the general transformation will be:
![]()
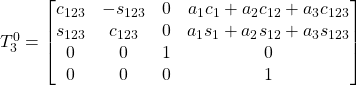
Spherical manipulator
Also for the spherical manipulator it is possible to create a table with the four Denavit-Hartenberg parameters for each base element. Here too we have 3 basic elements, but this time the transformation matrices will be different for each basic element.
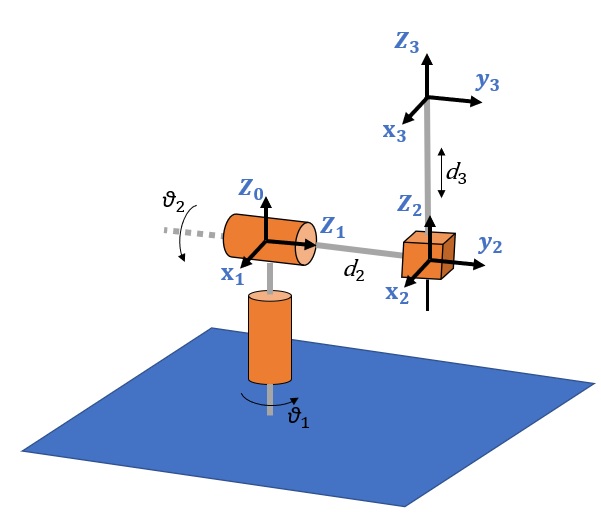
| BASE Element | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
The three transformation matrices of the coordinates corresponding to the single elements will therefore be the following:


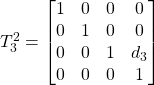
And so the general transformation matrix will be:
![]()

Anthropomorphic manipulator
Even for complex manipulators like the anthropomorphic one, the approach remains almost the same. Here, too, three basic elements are defined and the following table with the corresponding Denavit-Hartenberg properties.
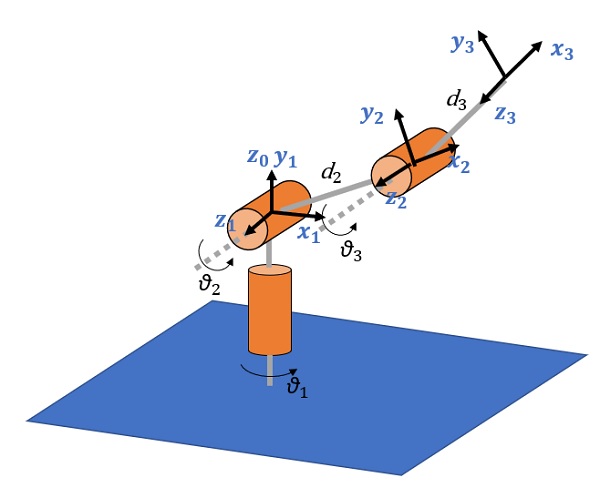
| BASE Element | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
The three coordinate transformation matrices are obtained from the table (two are equal).

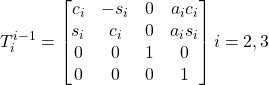
From the three transformation matrices of the basic elements we obtain the general one:
![]()

Spherical wrist
Another popular manipulator is the spherical wrist, often connected as an effective end to other manipulators.
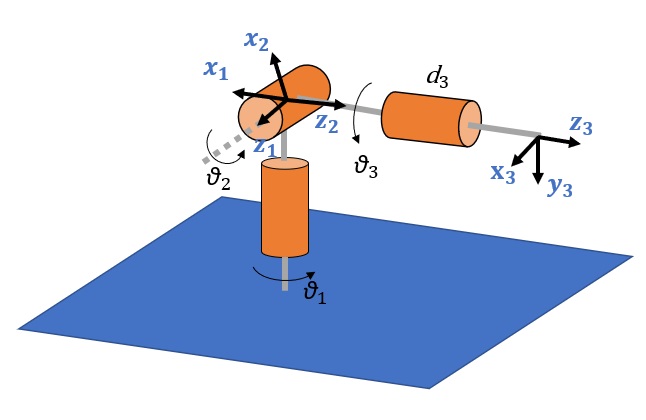
| BASE Element | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
The three coordinate transformation matrices are obtained from the table (two are equal).



From the three transformation matrices of the basic elements we obtain the general one:
![]()