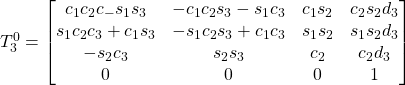Cinematica Diretta (Forward Kinematics)
La cinematica diretta (forward kinematics) ci pemette di determinare la posizione e l’orientamento dell’estremità efficiace (end-effector) in termini delle variabili dei giunti. Un modo semplice per spiegare la cinematica diretta è quella di prendere un caso molto semplice ed applicarci le metodologie base di questa tecnica.

Il manipolatore a 2 link e 2 giunti
Un caso molto semplice di robotica con cui applicare la cinematica diretta è il manipolatore a 2 link e 2 giunti. Ora il classico problema della cinematica diretta sarà quello, data la lunghezza dei link l1 ed l2 e gli angoli assunti dai due giunti θ1 e θ2, di ricavare la posizione dell’estremità efficace con le coordinate x e y.
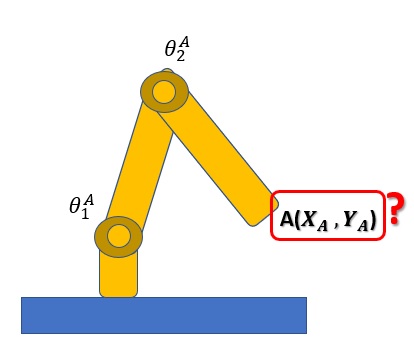
Nei casi pratici, spesso i manipolatori hanno al loro interno dei sensori che permettono di conoscere in tempo reale la posizione o l’angolo dei vari giunti. Quindi si darà per scontato la conoscenza dei valori dei due angoli θ1 e θ2 che si useranno come valori base per i nostri calcoli.
La prima cosa da fare sarà quello di stabilire un sistema fisso di coordinate, chiamato base frame. Nel caso dei manipolatori ci si riferisce alla base del manipolatore (estremità opposta all’estremità efficace) come base delle coordinate o0x0y0.
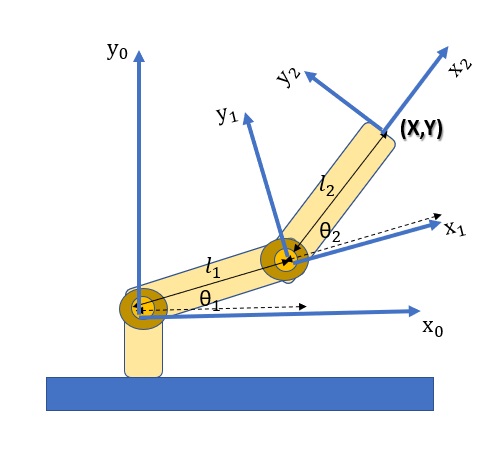
Le coordinate (x,y) del tool vengono espresse come:
![]()
![]()
In cui l1 e l2 sono le lunghezze dei due link. Anche l’orientamento del tool frame relativi al base frame viene dato dalla direzione dei coseni degli assi x2 e y2 rispetto agli assi x0 e y0.
![]()
![]()
![]()
![]()
Queste quattro equazioni possono essere combinate per ottenere una matrice di orientamento.
![]()
Le equazioni che abbiamo appena definito vengono chiamate le equazioni di cinematica diretta (forward kinematic equations) e sno specifiche del manipolatore preso in esame.
Casi più complessi – la procedura di Denavit-Hartenberg
Il caso del manipolatore a 2 link e 2 giunti è un esempio base, ma altri casi più avanzati posso portare ad equazioni troppo complesse e spesso non facilmente scrivibili.
In ogni caso, esiste una procedura generale che permette di stabilire un sistema di coordinate per ciascun giunto, per poi di passare da un sistema all’altro attraverso delle trasformazioni di matrici. Tale procedura viene chiamata procedura di Denavit-Hartenberg.
In tale procedura verranno usate delle coordinate omogenee e delle trasformazioni omogenee per semplificare la trasformazione tra i diversi sistemi di coordinate.
Esisono quindi delle convenzioni, dette appunto di Denavit-Hartenberg.
La numerazione dei link e dei giunti.
I link vengono numerati da 0 ad n partendo dalla base ed arrivando all’estremità efficace, e si indicano con ![]() . Si descrive così un manipolatore seriale con una catena di n+1 link. Questo manipolatore avrà di conseguenza n giunti, che si indicheranno a loro volta con
. Si descrive così un manipolatore seriale con una catena di n+1 link. Questo manipolatore avrà di conseguenza n giunti, che si indicheranno a loro volta con ![]() .
.
Il link ![]() sarà quello che collega il giunto
sarà quello che collega il giunto ![]() con quello
con quello ![]() .
.
Assegnazione degli assi z dei diversi sistemi di riferimento (frames).
Ad ogni link ![]() si associa un frame di coordinate solidale
si associa un frame di coordinate solidale ![]() il cui asse
il cui asse ![]() coincide con l’asse del giunto
coincide con l’asse del giunto ![]() , cioè del giunto a valle nella catena (quello più vicino all’estremità efficace). Essendo i giunti generalmente rotativi su di un piano, si indica con z, l’asse perpendicolare a questo piano.
, cioè del giunto a valle nella catena (quello più vicino all’estremità efficace). Essendo i giunti generalmente rotativi su di un piano, si indica con z, l’asse perpendicolare a questo piano.
L’elemento base: link-giunto
Quindi la procedura di Denavit-Hartenberg consiste principalmente di considerare come elemento base di un manipolatore, una coppia di giunti con il link che li unisce. Ad ogni elemento base così definito corrisponderà una matrice di trasformazione di coordinate

Si hanno quindi due giunti ![]() e
e ![]() ed il link
ed il link ![]() interposto, con insieme definiti i due sistemi di riferimento
interposto, con insieme definiti i due sistemi di riferimento ![]() e
e ![]() .
.
Nella scelta dei sistemi di riferimento si procede nel seguente modo:
- l’asse
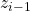 si sceglie coincidente con l’asse del giunto
si sceglie coincidente con l’asse del giunto 
- l’asse
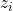 coincidente con l’asse del giunto
coincidente con l’asse del giunto 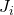 ;
; - l’asse
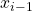 può essere scelto liberamente, ma è conveniente porlo in direzione del giunto successivo, e si interseca con
può essere scelto liberamente, ma è conveniente porlo in direzione del giunto successivo, e si interseca con 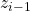 in corrispondenza del centro del giunto
in corrispondenza del centro del giunto  (scelto come origine);
(scelto come origine); - l’asse
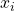 corre lungo la normale comune fra gli assi
corre lungo la normale comune fra gli assi 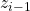 e
e 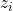
- gli assi
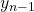 e
e 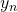 sono scelti in modo da completare le rispettive terne levogire.
sono scelti in modo da completare le rispettive terne levogire.
La trasformazione è allora descritta da quattro parametri di Denavit-Hartenberg:
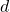 che è la distanza dell’asse
che è la distanza dell’asse 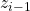 dalla normale comune; nel caso vi siano infinite normali comuni (assi
dalla normale comune; nel caso vi siano infinite normali comuni (assi 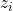 e e
e e 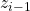 paralleli) si sceglierà il valore di
paralleli) si sceglierà il valore di 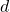 più conveniente;
più conveniente;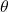 è l’angolo di rotazione intorno all’asse
è l’angolo di rotazione intorno all’asse 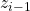 necessario per allineare
necessario per allineare  con
con 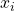 ;
; (a volte indicato anche con
(a volte indicato anche con  è la distanza minima fra gli assi
è la distanza minima fra gli assi 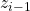 e
e 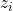 ;
;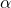 è l’angolo di rotazione intorno alla normale comune (ovvero attorno a
è l’angolo di rotazione intorno alla normale comune (ovvero attorno a 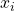 ) per allineare l’asse
) per allineare l’asse 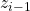 a
a 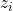 .
.
Si può notare che l’asse ![]() è perpendicolare sia all’asse
è perpendicolare sia all’asse ![]() che all’asse
che all’asse ![]() e interseca entrambi.
e interseca entrambi.
Trasformazione di coordinate
Ogni coppia braccio-giunto si può descrivere come un’operazione di trasformazione di coordinate fra i due sistemi di riferimento associati ai giunti.
Se si sceglie di orientare l’asse ![]() lungo la normale comune fra gli assi
lungo la normale comune fra gli assi ![]() e
e ![]() , la matrice di trasformazione è definita come una serie di due rototraslazioni consecutive:
, la matrice di trasformazione è definita come una serie di due rototraslazioni consecutive:
![]()
Dove

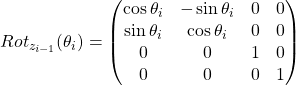

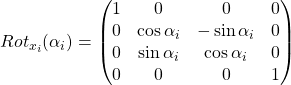
Da qui si ricava la matrice di trasformazione completa:
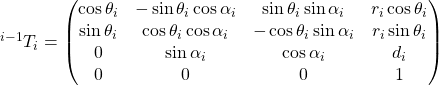
Adesso che conosciamo la matrice di trasformazione delle coordinate per ogni singolo elemento base link-giunto, è possibile applicare la dinamica diretta su qualsiasi tipo di manipolatore a catena. E’ sufficiente scomporre il manipolatore, per quanto complesso, nei suoi elementi base, calcolarsi le matrici di trasformazione per ciascun elemento, e poi moltiplicarli per ottenere una matrice generale.
Vediamo alcuni esempi di manipolatori più complessi.
Manipolatore planare a 3 bracci
Il manipolatore a tre bracci è formato da tre elementi base, i cui giunti ruotano tutti sullo stesso piano.
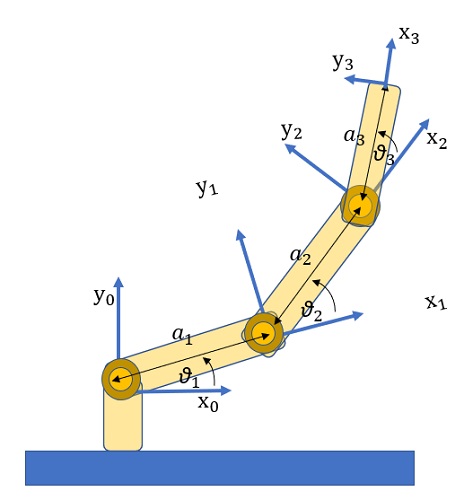
Per prima cosa quindi si definiscono i quattro parametri di Denavit-Hartenberg per ciascun elemento base e si riportano in una tabella.
| Elemento base | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
Dalla tabella degli elementi base si può vedere che le matrici di trasformazione saranno identiche:
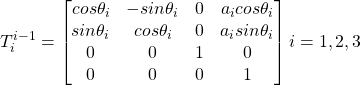
e quindi la trasformazione generale sarà:
![]()
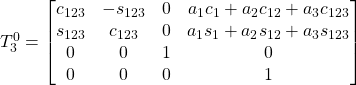
Manipolatore sferico
Anche per il manipolatore sferico è possibile creare una tabella con i quattro parametri di Denavit-Hartenberg per ciascun elemento base. Anche qui abbiamo 3 elementi base, ma questa volta le matrici di trasformazione saranno diverse per ciascun elemento base.
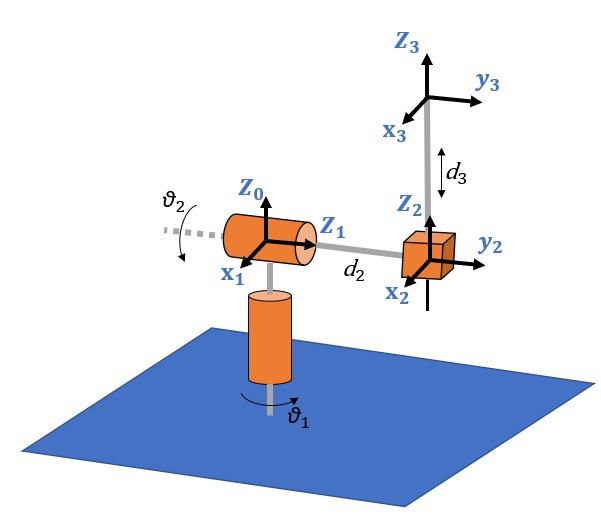
| Elemento base | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
Le tre matrici di trasformazione delle coordinate corrispondenti ai singoli elementi saranno quindi le seguenti:


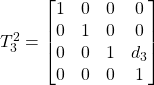
E quindi la matrice di trasformazione generale sarà:
![]()

Manipolatore antropomorfo
Anche per manipolatori complessi come quello antropomorfo, l’approccio rimane pressochè lo stesso. Anche qui si definiscono tre elementi basi e la seguente tabella con le corrispondenti proprietà di Denavit-Hartenberg.
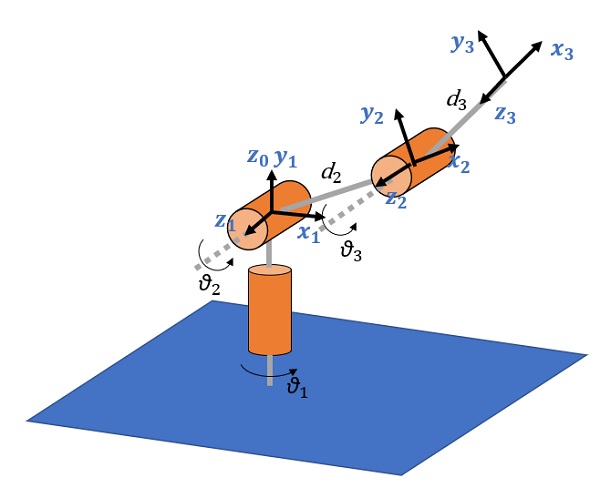
| Elemento base | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
Dalla tabella si ricavano le tre matrici di trasformazione delle coordinate (due sono uguali).

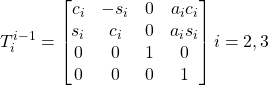
Dalle tre matrici di trasformazione degli elementi base si ricava quella generale:
![]()

Polso Sferico
Un altro manipolatore molto utilizzato è il polso sferico, spesso collegato come estremità efficace ad altri manipolatori.
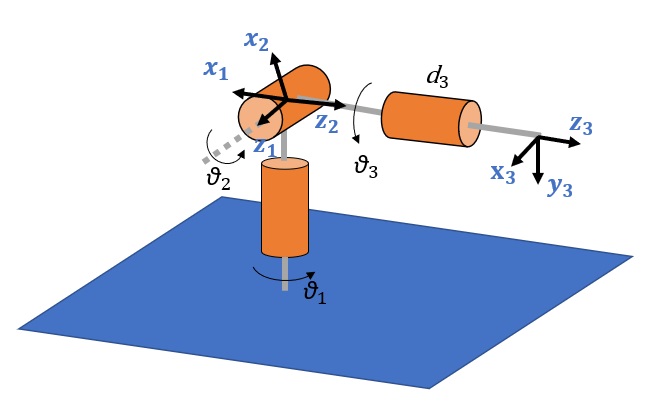
| Elemento base | ||||
|---|---|---|---|---|
| 1 | ||||
| 2 | ||||
| 3 |
Dalla tabella si ricavano le tre matrici di trasformazione delle coordinate (due sono uguali).



Dalle tre matrici di trasformazione degli elementi base si ricava quella generale:
![]()