Introduzione all'Hypothesis Testing: Esploriamo il Mondo delle Ipotesi Statistiche

Post Views: 624

L’Hypothesis Testing, o test di ipotesi, è uno strumento fondamentale nella statistica inferenziale che consente di prendere decisioni informate sulla base dei dati raccolti. Questa metodologia è ampiamente utilizzata in vari campi, dalla ricerca scientifica all’economia, dalla medicina all’ingegneria.

[wpda_org_chart tree_id=7 theme_id=50]

Cos’è l’Hypothesis Testing?

In termini semplici, l’Hypothesis Testing è un processo che consente di valutare affermazioni sulla popolazione basandosi su dati raccolti da un campione rappresentativo di quella popolazione. Si parte da due ipotesi:

Ipotesi Nulla 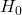$H_0$ : Afferma che non c’è alcun effetto o differenza rilevante. Di solito, rappresenta lo “status quo” o l’assenza di cambiamento.
Ipotesi Alternativa 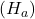$(H_a)$ : Propone che esista un effetto o una differenza rilevante. Può essere unilaterale (indicando una direzione specifica) o bilaterale (indicando semplicemente che c’è una differenza).

L’Ipotesi nulla

La “null hypothesis” (ipotesi nulla) gioca un ruolo fondamentale. L’ipotesi nulla, spesso indicata come $<em>H_</em>0$ , rappresenta uno stato di “status quo” o l’assenza di effetto. In altre parole, postula che non ci siano differenze o effetti osservabili in un determinato contesto. L’obiettivo dell’analisi delle ipotesi è valutare se c’è sufficiente evidenza nei dati per respingere questa ipotesi nulla a favore di un’ipotesi alternativa.

L’ipotesi alternativa

L’ipotesi alternativa (alternative hypothesis), spesso indicata come $H_a$ o $H_1$ , è la dichiarazione che cerca di suggerire un effetto, una differenza o un cambiamento significativo nella popolazione. In altre parole, rappresenta l’opposto dell’ipotesi nulla. Ad esempio, se l’ipotesi nulla afferma che non ci sono differenze significative, l’ipotesi alternativa potrebbe dichiarare che ci sono differenze effettive e misurabili.

Ci sono diverse forme di ipotesi alternative, a seconda della natura della domanda di ricerca. Alcuni esempi includono:

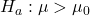$H_a: \mu > \mu_0$ – La media della popolazione è maggiore di un certo valore $\mu_0$ .
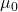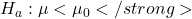$H_a: \mu < \mu_0</strong>$ – La media della popolazione è minore di un certo valore $\mu_0$ .

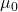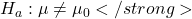$H_a: \mu \neq \mu_0</strong>$ – La media della popolazione è diversa da un certo valore 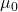$\mu_0$ . (bidirezionale).

Dove $\mu$ . rappresenta la media della popolazione. Questi esempi illustrano l’ipotesi alternativa per un test di ipotesi sulla media di una popolazione, ma possono essere adattati per altri tipi di test.

L’analisi delle ipotesi comporta la valutazione della evidenza nei dati per decidere se respingere l’ipotesi nulla in favore dell’ipotesi alternativa. La scelta tra le diverse forme di ipotesi alternative dipende dalla specificità della domanda di ricerca e dalla natura della relazione che si vuole testare.

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

Come Funziona?
Il processo di Hypothesis Testing segue un modello sistematico:

Formulazione delle Ipotesi: Si inizia con la definizione chiara dell’ipotesi nulla e dell’ipotesi alternativa, basandosi sulle aspettative e sulla domanda di ricerca.

Raccolta dei Dati: Vengono raccolti dati tramite esperimenti o osservazioni, cercando di ottenere un campione rappresentativo della popolazione di interesse.

Scelta del Test Statistico: A seconda della natura dei dati e della domanda di ricerca, si seleziona il test statistico appropriato. Ad esempio, il t-test può essere utilizzato per confrontare medie, mentre il chi-square test può essere utilizzato per analizzare la distribuzione di frequenza.

Determinazione del Significance Level 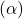$(\alpha)$ : Si fissa un livello di significatività, spesso a 0.05. Questo valore rappresenta la probabilità massima accettabile di commettere un errore di tipo I (respingere erroneamente l’ipotesi nulla).

Calcolo della Statistica di Test: Si calcola la statistica di test utilizzando i dati raccolti.

Decisione: Confrontando la statistica di test con la distribuzione di probabilità nota (sotto l’ipotesi nulla), si calcola il p-value, che rappresenta la probabilità di ottenere una statistica di test almeno tanto estrema quanto quella osservata. Se il p-value è inferiore al significance level, si può respingere l’ipotesi nulla.

Interpretazione: Si interpreta il risultato alla luce delle ipotesi formulate. Se l’ipotesi nulla viene respinta, si può concludere che ci sono prove sufficienti a supporto dell’ipotesi alternativa.

Il Significance Level
Il significance level, o livello di significatività, rappresenta la probabilità massima accettabile di commettere un errore di tipo I, ossia respingere erroneamente l’ipotesi nulla quando è effettivamente vera. È indicato spesso con il simbolo (\alpha).
Comunemente, il valore del significance level viene fissato a 0.05 o 5%. Questo significa che c’è una probabilità del 5% di erroneamente respingere l’ipotesi nulla quando è vera. Tuttavia, il valore di (\alpha) può essere scelto in base alle esigenze specifiche dello studio o della ricerca.
Se il p-value ottenuto dal test di ipotesi è inferiore al livello di significatività (\alpha), si ha sufficiente evidenza per respingere l’ipotesi nulla. D’altra parte, se il p-value è maggiore di (\alpha), non si dispone di prove sufficienti per respingere l’ipotesi nulla.
È importante notare che il significance level è una scelta soggettiva e può influenzare la natura delle conclusioni tratte dal test di ipotesi. Riducendo il significance level, si rende il test più conservativo, richiedendo prove più forti per respingere l’ipotesi nulla, ma aumentando il rischio di non rilevare effetti reali (errore di tipo II). Al contrario, aumentando il significance level, si rende il test meno conservativo, facilitando la rilevazione di effetti, ma aumentando il rischio di respingere erroneamente l’ipotesi nulla (errore di tipo I). La scelta del livello di significatività è quindi una questione di bilanciamento tra questi due tipi di errori e delle conseguenze pratiche delle decisioni basate sul test di ipotesi.

Esempio Pratico di Hypothesis Testing con Python
Immaginiamo di condurre un esperimento su un nuovo farmaco e vogliamo testare se il farmaco è efficace nel ridurre la pressione sanguigna. Le nostre ipotesi potrebbero essere:

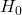$H_0$ : Il farmaco non ha effetto sulla pressione sanguigna $( \mu = 0 )$

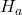$H_a$ : Il farmaco riduce la pressione sanguigna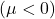 $( \mu < 0 )$

Dopo aver raccolto i dati e calcolato la statistica di test:
Ponendo il valore di significance level a 0.05

se 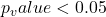$p_value < 0.05$ allora vale l’ipotesi alternativa $H_a$ ,

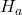se 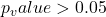$p_value > 0.05$ allora vale l’ipotesi nulla $H_0$ .

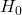Vediamo un esempio di codice Python che simula un esperimento con un farmaco e testa se il farmaco ha un effetto significativo sulla pressione sanguigna. Useremo la libreria numpy per generare dati casuali e matplotlib per creare un grafico illustrativo.
import numpy as np import matplotlib.pyplot as plt from scipy.stats import ttest_1samp # Simuliamo i dati della pressione sanguigna prima e dopo l'assunzione del farmaco np.random.seed(42) # Per rendere i risultati riproducibili before = np.random.normal(loc=120, scale=10, size=100) after = before - np.random.normal(loc=5, scale=2, size=100) # Eseguiamo il test t t_statistic, p_value = ttest_1samp(after - before, 0) # Impostiamo il livello di significatività a 0.05 alpha = 0.05 # Creiamo un grafico per visualizzare i dati plt.figure(figsize=(10, 6)) # Grafico delle distribuzioni prima e dopo il farmaco plt.hist(before, bins=20, alpha=0.5, label='Prima del Farmaco') plt.hist(after, bins=20, alpha=0.5, label='Dopo il Farmaco') plt.title('Distribuzione della Pressione Sanguigna Prima e Dopo il Farmaco') plt.xlabel('Pressione Sanguigna') plt.ylabel('Frequenza') plt.legend() plt.show() # Stampiamo il risultato del test if p_value < alpha: print("Reject the null hypothesis. Il farmaco ha un effetto significativo sulla pressione sanguigna.") else: print("Fail to reject the null hypothesis. Non ci sono prove sufficienti per affermare che il farmaco abbia un effetto significativo sulla pressione sanguigna.")
In questo esempio, stiamo simulando i dati della pressione sanguigna prima e dopo l’assunzione del farmaco, eseguendo un test t unilaterale a sinistra e creando un grafico delle distribuzioni dei dati. Infine, il test di ipotesi viene eseguito, e il risultato viene stampato insieme al grafico. Ricorda che i dati simulati sono solo a scopo illustrativo e potrebbero non riflettere la realtà.

Libro consigliato:

Se ti piace quest’argomento, ti consiglio questo libro:

Fondamenti di Statistica per Data Scientists

Altri Hypothesis Testing con Python
Vediamo un esempio di codice Python che esegue un test t bilaterale sulla media di un campione. In questo caso, consideriamo un campione di dati e vogliamo testare se la sua media è significativamente diversa da un valore di riferimento:
import numpy as np from scipy.stats import ttest_1samp # Generiamo un campione di dati (sostituisci questo con i tuoi dati reali) data_sample = np.random.normal(loc=5, scale=2, size=30) # Definiamo l'ipotesi nulla: la media è uguale a 4 null_hypothesis_mean = 4 # Definiamo l'ipotesi alternativa: la media è diversa da 4 (bidirezionale) alternative_hypothesis = "two-sided" # Eseguiamo il test t t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean) # Impostiamo il livello di significatività (solitamente 0.05) alpha = 0.05 # Confrontiamo il p-value con il livello di significatività if p_value < alpha: print("Reject the null hypothesis. There is enough evidence to suggest a significant difference.") else: print("Fail to reject the null hypothesis. There is not enough evidence to suggest a significant difference.")
Eseguendo il codice si ottiene:
Reject the null hypothesis. There is enough evidence to suggest a significant difference.
In questo esempio, l’ipotesi nulla $H_0$ afferma che la media della popolazione è uguale a 4, mentre l’ipotesi alternativa ((H_a)) è bidirezionale, indicando che la media è diversa da 4. Il test t viene eseguito, e in base al p-value confrontato con il livello di significatività, decidiamo se respingere l’ipotesi nulla o meno.
La Critical Region
La “critical region” (regione critica) è la gamma di valori di una statistica di test che porterebbe al rifiuto dell’ipotesi nulla durante un test di ipotesi. In altre parole, è l’insieme di risultati che sono così estremi da suggerire che l’ipotesi nulla non è valida.
La decisione di respingere l’ipotesi nulla si basa sulla comparazione tra la statistica di test calcolata dai dati e una soglia critica corrispondente al livello di significatività ((\alpha)) prescelto. Se la statistica di test cade nella regione critica, respingiamo l’ipotesi nulla; altrimenti, non la respingiamo.
Ad esempio, nel contesto di un test t univariato, la regione critica potrebbe essere la coda superiore e inferiore della distribuzione t in base al valore di (\alpha) selezionato. Se la statistica di test cade in una di queste code, respingiamo l’ipotesi nulla.
La scelta della regione critica dipende dal tipo di test (unilaterale o bilaterale) e dal significance level scelto. È un concetto chiave nella conduzione e interpretazione dei test di ipotesi, poiché aiuta a definire i confini oltre i quali si ritiene che le osservazioni siano così estreme da non essere spiegate semplicemente dal caso, ma piuttosto indicano un effetto significativo.
Il p-value ed il q-value
Il p-value e il q-value sono entrambi misure utilizzate in statistica, ma hanno scopi leggermente diversi.
p-value:
Il p-value, o valore di probabilità, è una misura che indica la probabilità di ottenere un risultato altrettanto estremo o più estremo di quello osservato, sotto l’ipotesi nulla. In altre parole, il p-value fornisce un’indicazione su quanto le tue osservazioni siano incompatibili con l’ipotesi nulla. Se il p-value è inferiore al tuo livello di significatività (spesso 0.05), si può decidere di respingere l’ipotesi nulla.
# Esempio di ottenimento del p-value da un test t from scipy.stats import ttest_1samp data_sample = [3, 4, 5, 6, 7] null_hypothesis_mean = 4.5 t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean) print(f"P-value: {p_value}")
Eseguendo si ottiene:
P-value: 0.5185185185185183
q-value:
Il q-value, o valore di correzione per i tassi di falsi positivi, è spesso utilizzato in contesti in cui vengono effettuati molti test simultaneamente. Ad esempio, quando si eseguono test multipli (test di molte ipotesi simultaneamente), il q-value aiuta a controllare il tasso di falsi positivi (errore di tipo I) tenendo conto del numero di test effettuati. Un q-value basso indica che un risultato è statisticamente significativo, anche dopo la correzione per i test multipli.
# Esempio di ottenimento del q-value con correzione di FDR (False Discovery Rate) from statsmodels.stats.multitest import multipletests # Lista di p-value ottenuti da test multipli p_values = [0.03, 0.12, 0.04, 0.09] # Correzione di FDR reject, q_values, _, _ = multipletests(p_values, method='fdr_bh') print(f"Q-values: {q_values}")
Eseguendo si ottiene:
Q-values: [0.08 0.12 0.08 0.12]
In sintesi, mentre il p-value è una misura della probabilità che i tuoi dati siano compatibili con l’ipotesi nulla, il q-value è utilizzato per correggere i tassi di errore quando vengono eseguiti molti test simultaneamente.
Tailed Test
Un tailed test, o test unilaterale, è un tipo di test di ipotesi in cui la regione critica è situata solo su uno dei lati della distribuzione della statistica di test. Esistono due tipi principali di test unilaterali:

Unilaterale a sinistra (Left-tailed): La regione critica è nella coda sinistra della distribuzione. Questo tipo di test è utilizzato quando si vuole testare se la statistica di test è significativamente più bassa di un certo valore.

Unilaterale a destra (Right-tailed): La regione critica è nella coda destra della distribuzione. Questo tipo di test è utilizzato quando si vuole testare se la statistica di test è significativamente più alta di un certo valore.

Per esempio, considera un test t su una media di un campione:

Un tailed test a sinistra potrebbe essere utilizzato per verificare se la media del campione è significativamente inferiore a un certo valore.

Un tailed test a destra potrebbe essere utilizzato per verificare se la media del campione è significativamente superiore a un certo valore.

Ecco un esempio di unilaterale a destra con il modulo scipy.stats in Python:
from scipy.stats import ttest_1samp data_sample = [3, 4, 5, 6, 7] null_hypothesis_mean = 4.5 # Test unilaterale a destra t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean) print(f"P-value: {p_value/2}") # Dividiamo per 2 per ottenere il p-value corretto per il test unilaterale
Nel test unilaterale a destra, il p-value viene diviso per 2 perché stiamo interessati solo a una coda della distribuzione.
P-value: 0.25925925925925913
I test unilaterali sono appropriati quando c’è un interesse specifico a rilevare un cambiamento in una particolare direzione, ad esempio, se ci aspettiamo che la statistica di test sia più grande o più piccola di un certo valore di riferimento.
Two-Tailed Test
Il two-tailed test, o test bilaterale, è un tipo di test di ipotesi in cui la regione critica è divisa tra entrambe le code della distribuzione della statistica di test. Questo tipo di test è utilizzato quando si vuole valutare se la statistica di test è significativamente diversa da un certo valore, senza specificare in quale direzione.
Un esempio comune di un two-tailed test è quando si desidera testare se la media di un campione è diversa da un certo valore. In questo caso, si cerca di identificare se ci sono prove sufficienti per concludere che la media del campione è significativamente più alta o più bassa rispetto al valore specificato.
Ecco un esempio di two-tailed test con il modulo scipy.stats in Python:
from scipy.stats import ttest_1samp data_sample = [3, 4, 5, 6, 7] null_hypothesis_mean = 4.5 # Test bilaterale t_statistic, p_value = ttest_1samp(data_sample, null_hypothesis_mean) print(f"P-value: {p_value}")
In un two-tailed test, il p-value fornito rappresenta la probabilità che la statistica di test sia così estrema o più estrema, sia nella coda superiore che in quella inferiore della distribuzione, sotto l’ipotesi nulla.
P-value: 0.5185185185185183
Se il p-value è inferiore al livello di significatività prescelto (solitamente 0.05), si può concludere che ci sono prove sufficienti per respingere l’ipotesi nulla, indicando che la statistica di test è significativamente diversa dal valore specificato.
Conclusioni
L’Hypothesis Testing fornisce un quadro metodologico per prendere decisioni sulla base dei dati, introducendo rigorosità scientifica nelle analisi statistiche. La sua applicazione corretta contribuisce alla validità e alla robustezza delle conclusioni tratte dalla ricerca, garantendo che le affermazioni fatte siano supportate da prove solide.