La distribuzione t di Student con Python

La distribuzione t di Student è una distribuzione di probabilità che deriva dal concetto di t-statistica. È spesso utilizzata in inferenza statistica quando il campione su cui si basa un’analisi è relativamente piccolo e la deviazione standard della popolazione è sconosciuta. La forma della distribuzione t è simile a quella normale, ma ha code più spesse, il che la rende più adatta per campioni di dimensioni ridotte.

Questa distribuzione è ampiamente utilizzata nei test t e negli intervalli di confidenza, specialmente quando si tratta di stime sulla media di una popolazione. La forma esatta della distribuzione t dipende dai gradi di libertà, che sono determinati dalla dimensione del campione. Con l’aumentare dei gradi di libertà, la distribuzione t si avvicina sempre di più a una distribuzione normale standard.

[wpda_org_chart tree_id=8 theme_id=50]

Distribuzione t di Student

La distribuzione t di Student viene ottenuta introducendo una correzione per la variabilità aggiuntiva dovuta a campioni di dimensioni ridotte quando si stima la deviazione standard della popolazione.

L’idea di base è legata al concetto di t-statistica, che è data da:

dove:

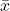• è la media del campione,
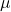• è la media della popolazione,
• è la deviazione standard del campione,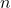
• è la dimensione del campione.

La distribuzione di questa t-statistica segue la distribuzione t di Student. La forma esatta della distribuzione t dipende dai gradi di libertà , che sono calcolati come , dove è la dimensione del campione.

Quando i gradi di libertà aumentano, la distribuzione t si avvicina alla distribuzione normale standard. Questo significa che all’aumentare delle dimensioni del campione, la correzione per la dimensione del campione diventa meno critica, e la distribuzione t si comporta sempre più come una distribuzione normale.

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

Utilizzo della distribuzione di t di Student

La distribuzione t di Student viene comunemente utilizzata in vari contesti, specialmente quando si lavora con campioni di dimensioni ridotte o quando la deviazione standard della popolazione è sconosciuta. Ecco alcuni esempi concreti:

• Test t per una singola media:

Supponiamo di avere un piccolo campione di dimensione 10 e vogliamo testare se la media del campione è significativamente diversa da una certa media teorica.

• Test t per differenze tra due medie:

Quando confrontiamo due gruppi con campioni di dimensioni limitate e vogliamo determinare se le loro medie sono significativamente diverse.

• Intervallo di confidenza per la media:

Calcolare un intervallo di confidenza per stimare la media della popolazione, specialmente quando la deviazione standard della popolazione è sconosciuta.

• Regressione lineare:

Nei casi in cui si esegue una regressione lineare con un piccolo numero di osservazioni, i test sulla significatività dei coefficienti possono coinvolgere la distribuzione t.

• Analisi della varianza (ANOVA):

Quando confrontiamo le medie di più di due gruppi e i campioni hanno dimensioni ridotte, la distribuzione t può essere coinvolta nella valutazione della significatività delle differenze tra i gruppi.

In sostanza, la distribuzione t è uno strumento prezioso quando si lavora con campioni di piccole dimensioni e si desidera effettuare inferenze sulla popolazione da cui provengono i campioni.

Libro consigliato:

Se ti piace quest’argomento, ti consiglio questo libro:

Fondamenti di Statistica per Data Scientists

Esempio di utilizzo di t di Student

Consideriamo un esempio in cui vogliamo calcolare la distribuzione t per un test t su una singola media. Supponiamo di avere un campione di dimensione 15 e vogliamo testare se la media di questo campione è significativamente diversa da 10. La media del campione è 9, la deviazione standard del campione è 2.5.

Calcolo della t-statistica:

Calcolo dei gradi di libertà:

Distribuzione t di Student:
Ora possiamo guardare la tabella della distribuzione t di Student o utilizzare software statistici per ottenere il p-value associato a e . Supponiamo che otteniamo un p-value di .

Puoi utilizzare il modulo scipy.stats in Python per eseguire il calcolo della t-statistica e ottenere il p-value. Ecco un esempio di codice Python per l’esempio che abbiamo discusso:

import numpy as np
from scipy import stats

# Dati del campione
sample_mean = 9
population_mean = 10
sample_std = 2.5
sample_size = 15

# Calcolo della t-statistica
t_statistic = (sample_mean - population_mean) / (sample_std / np.sqrt(sample_size))

# Calcolo dei gradi di libertà
degrees_of_freedom = sample_size - 1

# Calcolo del p-value
p_value = 2 * stats.t.cdf(t_statistic, df=degrees_of_freedom)

# Stampa dei risultati
print(f"t-statistica: {t_statistic}")
print(f"Gradi di libertà: {degrees_of_freedom}")
print(f"P-value: {p_value}")

Eseguendo otterrai il seguente risultato:

t-statistica: -1.5491933384829668
Gradi di libertà: 14
P-value: 0.1436400002452211

Assicurati di avere il modulo scipy installato. Puoi installarlo usando:

pip install scipy

Questo codice calcola la t-statistica, i gradi di libertà e il p-value associato. Ricorda che il p-value è la probabilità di ottenere un risultato almeno così estremo quanto quello osservato, assumendo che l’ipotesi nulla (nel nostro caso, che le medie sono uguali) sia vera. Se il p-value è inferiore al livello di significatività scelto (ad esempio, 0.05), possiamo respingere l’ipotesi nulla.

Possiamo rappresentare graficamente la distribuzione t utilizzando un grafico a densità della distribuzione t. La forma della distribuzione t dipenderà dai gradi di libertà. A causa della sua forma a campana e delle code più spesse rispetto a una normale, la distribuzione t sarà diversa in base ai gradi di libertà. Ad esempio, potremmo disegnare la distribuzione t con 14 gradi di libertà e sovrapporla a una normale standard per mostrare le differenze nelle code. ribuzione normale.

Puoi utilizzare il modulo matplotlib per visualizzare le distribuzioni. Ecco un esempio di codice che crea un grafico della distribuzione t con 14 gradi di libertà e la sovrappone a una distribuzione normale standard:

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import t, norm

# Gradi di libertà
degrees_of_freedom = 14

# Genera dati per la distribuzione t
x = np.linspace(-4, 4, 1000)
y_t = t.pdf(x, df=degrees_of_freedom)

# Genera dati per la distribuzione normale standard
y_norm = norm.pdf(x)

# Crea il grafico
plt.figure(figsize=(10, 6))
plt.plot(x, y_t, label=f't-distribution (df={degrees_of_freedom})')
plt.plot(x, y_norm, label='Standard Normal Distribution', linestyle='dashed')
plt.title('Distribuzione t vs Distribuzione Normale Standard')
plt.xlabel('Valore della variabile casuale')
plt.ylabel('Densità di probabilità')
plt.legend()
plt.grid(True)
plt.show()

Libro Suggerito:

Se sei interessato all’argomento, ti suggerisco di leggere questo libro:

Practical Statistics for Data Scientists

Questo codice crea un grafico che mostra la distribuzione t con 14 gradi di libertà e la sovrappone a una distribuzione normale standard (linea tratteggiata). Puoi notare come le code della distribuzione t siano più spesse rispetto a quelle della distribuzione normale standard.