La Probabilty Density Function (PDF) con Python

Post Views: 917

La Probability Density Function (PDF) è una funzione matematica che descrive la probabilità relativa di una variabile casuale di assumere determinati valori. In altre parole, fornisce una rappresentazione della distribuzione di probabilità di una variabile continua. La PDF è non negativa e l’area sotto la curva corrisponde a 1, poiché rappresenta la probabilità totale. Ad esempio, nella distribuzione normale, la PDF è rappresentata da una curva a campana.

[wpda_org_chart tree_id=8 theme_id=50]

La Funzione di Densità di Probabilità

La Probability Density Function (PDF) è una funzione che descrive la distribuzione di probabilità di una variabile casuale continua. La PDF è spesso indicata con (f(x)), dove (x) rappresenta il valore della variabile casuale.

Equazione della PDF:
La forma specifica dell’equazione dipende dalla distribuzione della variabile casuale. Per esempio, per la distribuzione normale standard, la PDF è:

$f(x) = \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$

Dove:

$\pi$ è il valore di Pi (circa 3.14159),
$e$ è la base del logaritmo naturale (circa 2.71828),
$\frac{1}{\sqrt{2\pi}}$ è una costante di normalizzazione.

Questa PDF descrive la forma della classica campana gaussiana.La PDF è quindi uno strumento chiave per comprendere e lavorare con variabili casuali continue, consentendo di effettuare previsioni, calcolare probabilità e analizzare la forma della distribuzione di probabilità.

La derivazione della PDF dipende dalla distribuzione specifica della variabile casuale. In alcuni casi, può essere derivata dalla funzione di densità di probabilità (Probability Density Function) o dalla funzione di ripartizione cumulativa (Cumulative Distribution Function).

Utilità della PDF

Calcolo di Probabilità: L’area sotto la curva della PDF in un intervallo corrisponde alla probabilità che la variabile casuale cada in quell’intervallo. Questo viene ottenuto integrando la PDF su quell’intervallo.
Calcolo di Statistiche: La PDF consente di calcolare diverse statistiche, come la media e la varianza, integrando le espressioni adeguate sulla PDF.
Predizioni e Analisi: La forma della PDF fornisce informazioni sulla distribuzione della variabile casuale. Ad esempio, nella distribuzione normale, una PDF a forma di campana indica che i valori centrali sono più probabili rispetto a quelli estremi.
Confronto di Distribuzioni: Può essere utilizzata per confrontare distribuzioni diverse e comprendere come cambiano le probabilità in diverse regioni della variabile casuale.

In sostanza, la PDF è uno strumento fondamentale per comprendere e lavorare con variabili casuali continue, fornendo una descrizione dettagliata della distribuzione di probabilità e consentendo una vasta gamma di analisi statistiche.

Libro consigliato:

Se ti piace quest’argomento, ti consiglio questo libro:

Fondamenti di Statistica per Data Scientists

Alcuni esempi in Python

Ecco alcuni esempi di codice che coinvolgono la Probability Density Function (PDF) per alcune distribuzioni comuni utilizzando il linguaggio Python con la libreria SciPy:

Distribuzione Normale

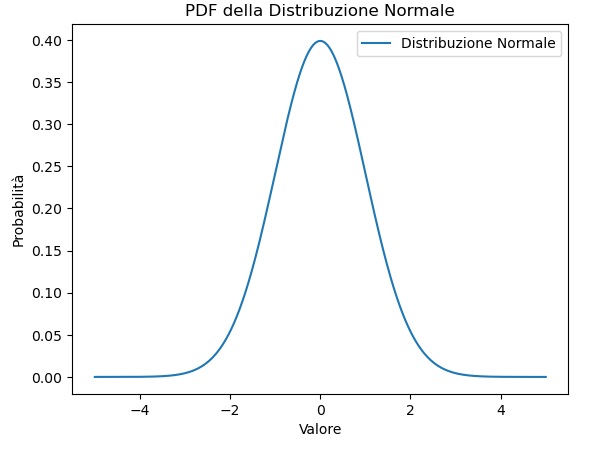
La distribuzione di probabilità più comunemente usata è quella della distribuzione normale. Il codice seguente ci permette di calcolarla e visualizzarla in un grafico.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

mu, sigma = 0, 1  # Media e deviazione standard
x = np.linspace(-5, 5, 1000)
pdf = norm.pdf(x, mu, sigma)

plt.plot(x, pdf, label='Distribuzione Normale')
plt.title('PDF della Distribuzione Normale')
plt.xlabel('Valore')
plt.ylabel('Probabilit&agrave;')
plt.legend()
plt.show()

Eseguendo il codice si ottiene il grafico seguente che corrisponde alla PDF della distribuzione normale

Distribuzione Uniforme

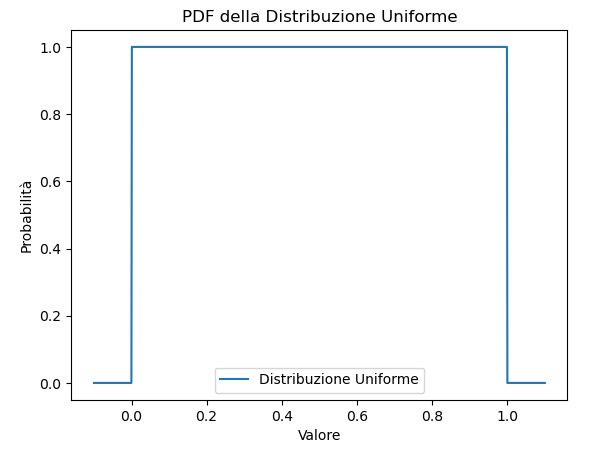
Un’altra funzione di distribuzione di probabilità molto nota e utilizzata è quella relativa alla distribuzione uniforme. La PDF per una variabile casuale (X) con distribuzione uniforme tra (a) e (b) è definita come segue:

$f(x; a, b) = \frac{1}{b - a}$

dove $a$ e $b$ sono i parametri che definiscono l’intervallo di supporto della distribuzione uniforme, e (x) è un valore all’interno di questo intervallo. La PDF è zero al di fuori di questo intervallo.

Questa equazione rappresenta la densità di probabilità costante tra $a$ e $b$ , il che significa che ogni punto all’interno di questo intervallo ha la stessa probabilità di essere campionato.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import uniform

a, b = 0, 1  # Estremi dell'intervallo
x = np.linspace(a - 0.1, b + 0.1, 1000)
pdf = uniform.pdf(x, a, b - a)

plt.plot(x, pdf, label='Distribuzione Uniforme')
plt.title('PDF della Distribuzione Uniforme')
plt.xlabel('Valore')
plt.ylabel('Probabilit&agrave;')
plt.legend()
plt.show()

Eseguendo si ottiene il grafico seguente.

Libro Suggerito:

Se sei interessato all’argomento, ti suggerisco di leggere questo libro:

Practical Statistics for Data Scientists

Distribuzione Esponenziale

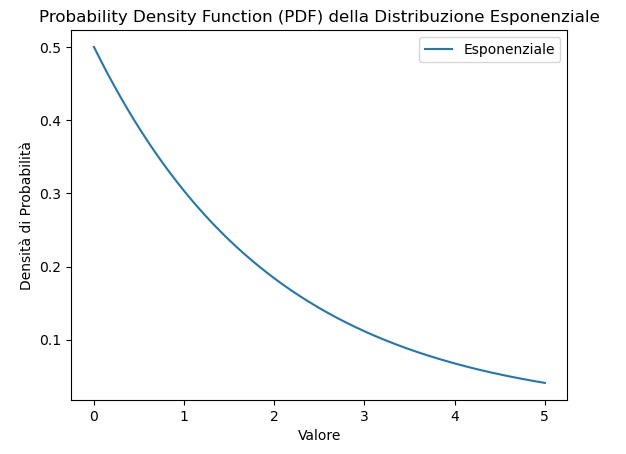
Un’altra distribuzione molto utilizzata è quella esponenziale. La PDF per una variabile casuale (X) con distribuzione esponenziale è data da:

$f(x; \lambda) = \lambda e^{-\lambda x}$

Dove $x \geq 0$ e $\lambda > 0$ è il parametro di scala.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import expon

# Parametro della distribuzione esponenziale
lambda_param = 0.5

x = np.linspace(0, 5, 1000)
pdf = expon.pdf(x, scale=1/lambda_param)

plt.plot(x, pdf, label='Esponenziale')
plt.title('Probability Density Function (PDF) della Distribuzione Esponenziale')
plt.xlabel('Valore')
plt.ylabel('Densit&agrave; di Probabilit&agrave;')
plt.legend()
plt.show()

Eseguendo il codice si ottiene la rappresentazione della PDF nel grafico seguente.

Distribuzione Gamma

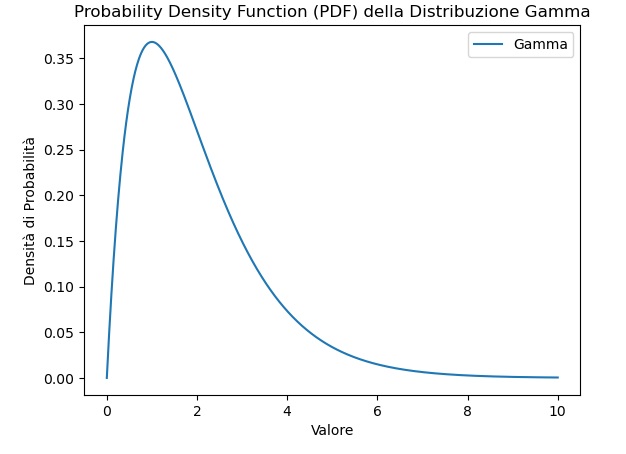
Un’altra distribuzione ancora è quella gamma. Ecco anche in questo caso il codice per poter ottenere la sua PDF. La PDF per una variabile casuale $X$ con distribuzione gamma è data da:

$f(x; \alpha, \beta) = \frac{\beta^\alpha x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)}$

Dove $x \geq 0$ , $\alpha > 0$ è il parametro di forma, $\beta > 0$ è il parametro di scala, e $\Gamma(\alpha)$ è la funzione gamma.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma

# Parametri della distribuzione gamma
alpha = 2
beta = 1

x = np.linspace(0, 10, 1000)
pdf = gamma.pdf(x, alpha, scale=1/beta)

plt.plot(x, pdf, label='Gamma')
plt.title('Probability Density Function (PDF) della Distribuzione Gamma')
plt.xlabel('Valore')
plt.ylabel('Densit&agrave; di Probabilit&agrave;')
plt.legend()
plt.show()

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

Distribuzione Log-Normale

Vediamo per concludere, anche la funzione di distribuzione di probabilità Log-Normale. La PDF per una variabile casuale (X) con distribuzione log-normale è data da:

$f(x; \mu, \sigma) = \frac{1}{x\sigma \sqrt{2\pi}} e^{-\frac{(\ln(x) - \mu)^2}{2\sigma^2}}$

Dove $x > 0$ , $\mu$ è la media del logaritmo, $\sigma$ è la deviazione standard del logaritmo.

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import lognorm

# Parametri della distribuzione log-normale
mu = 0
sigma = 0.1

x = np.linspace(0, 3, 1000)
pdf = lognorm.pdf(x, sigma, scale=np.exp(mu))

plt.plot(x, pdf, label='Log-Normale')
plt.title('Probability Density Function (PDF) della Distribuzione Log-Normale')
plt.xlabel('Valore')
plt.ylabel('Densit&agrave; di Probabilit&agrave;')
plt.legend()
plt.show()

Questi sono solo alcuni esempi di distribuzioni continue che si possono esplorare utilizzando la libreria SciPy in Python. Ogni distribuzione ha i suoi parametri specifici che possono essere adattati in base alle esigenze dell’analisi.

La Funzione di Densità di Probabilità

Utilità della PDF

Libro consigliato:

Alcuni esempi in Python

Lascia un commento Annulla risposta