Skewness con Python - Meccanismo Complesso

Post Views: 699

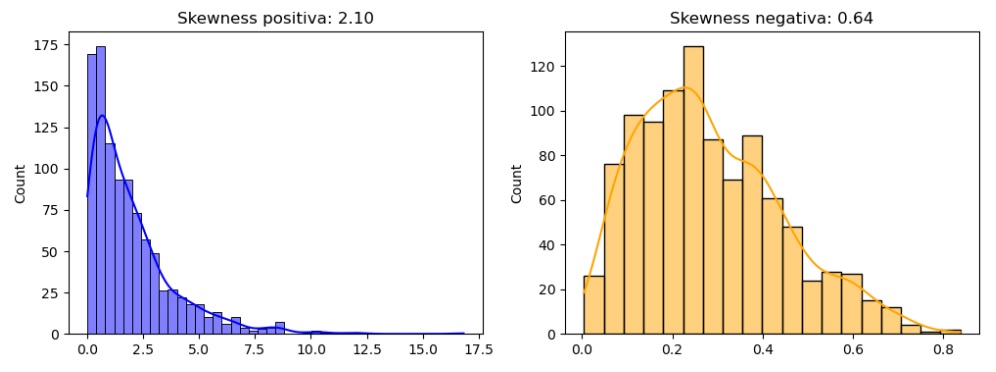
La skewness è una misura statistica che descrive l’asimmetria della distribuzione di un insieme di dati. Indica se la coda della distribuzione è spostata verso sinistra o verso destra rispetto alla sua parte centrale. Una skewness positiva indica una coda più lunga a destra, mentre una skewness negativa indica una coda più lunga a sinistra.

[wpda_org_chart tree_id=15 theme_id=50]

La Skewness

La skewness è una misura cruciale che ci aiuta a comprendere quanto i nostri dati siano inclinati verso sinistra o destra rispetto alla loro media. Quando la skewness è positiva, ci suggerisce che potrebbero esserci valori eccezionalmente alti influenzando la coda destra della distribuzione. Al contrario, una skewness negativa indica una coda più lunga a sinistra, suggerendo possibili valori outlier inferiori. Questa informazione è fondamentale nell’analisi dei dati poiché fornisce insight sulla forma della distribuzione, orientando anche la scelta di tecniche statistiche adeguate e facilitando la predizione del comportamento futuro dei dati. Inoltre, la skewness è utile nel rilevare outlier, confrontare distribuzioni e descrivere la concentrazione dei dati attorno alla media. In sintesi, è uno strumento prezioso per interpretare la struttura dei dati e guidare analisi statistiche informate.

La skewness può essere misurata utilizzando diverse formule, ma una delle più comuni è la formula del momento del terzo ordine. Se denotiamo la skewness come (g_1), la formula è:

$g_1 = \frac{\frac{1}{n} \sum_{i=1}^{n}(X_i - \bar{X})^3}{\left(\frac{1}{n} \sum_{i=1}^{n}(X_i - \bar{X})^2\right)^{3/2}}$

Dove:

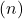$(n)$ è il numero di osservazioni nei dati.
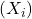$(X_i)$ è ciascuna osservazione.
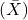$(\bar{X})$ è la media dei dati.

Questa formula confronta il momento del terzo ordine (skewness) con il quadrato del momento del secondo ordine (varianza). La skewness sarà positiva se la distribuzione è asimmetrica a destra, negativa se è asimmetrica a sinistra, e zero se è perfettamente simmetrica.

A cosa serve conoscere la Skewness

Conoscere la skewness di una distribuzione è utile in statistica per comprendere la forma e l’asimmetria dei dati. Ecco alcune ragioni per cui è importante:

Descrizione della distribuzione: La skewness fornisce informazioni sulla forma della distribuzione dei dati. Una skewness diversa da zero indica che la distribuzione non è simmetrica.
Predizione di comportamenti: Può aiutare a prevedere come si comporteranno i dati. Ad esempio, una skewness positiva suggerisce la presenza di code più lunghe a destra, indicando la possibilità di valori estremamente alti.
Selezione delle tecniche statistiche: La conoscenza della skewness può influenzare la scelta delle tecniche statistiche appropriate. Alcuni metodi statistici assumono una distribuzione simmetrica, quindi la skewness può influenzare l’interpretazione dei risultati.
Rilevazione di anomalie: In alcuni casi, una skewness significativa può indicare la presenza di anomalie o dati outliers che potrebbero influenzare l’analisi.

In generale, la skewness è uno strumento utile per ottenere una comprensione più approfondita della struttura e della tendenza centrale di un insieme di dati.

Un esempio di calcolo di Skewness

In Python, puoi utilizzare la libreria scipy per calcolare la skewness di un insieme di dati. Ecco un esempio di come farlo:

import numpy as np
from scipy.stats import skew

# Creare un insieme di dati di esempio
dati = np.array([1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5])

# Calcolare la skewness
skewness = skew(dati)

# Stampare il risultato
print("Skewness:", skewness)

In questo esempio, ho utilizzato un semplice insieme di dati, ma puoi sostituire l’array dati con il tuo insieme di dati. La funzione skew restituirà la skewness calcolata per quei dati. Eseguendo il codice si otterrà il seguente risultato:

Skewness: -0.5879747322073333

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:

Python Data Analytics 3rd Ed

Fabio Nelli

Alcuni esempi di applicazione della Skewness

Skewness nello studio di una distribuzione

Ecco un esempio su come puoi utilizzare Python per calcolare la skewness e descrivere la forma di una distribuzione:

import numpy as np
from scipy.stats import skew
import matplotlib.pyplot as plt
import seaborn as sns

# Creare un insieme di dati con una skewness positiva
dati_positivi = np.random.exponential(scale=2, size=1000)

# Creare un insieme di dati con una skewness negativa
dati_negativi = np.random.beta(a=2, b=5, size=1000)

# Calcolare la skewness per entrambi gli insiemi di dati
skewness_positiva = skew(dati_positivi)
skewness_negativa = skew(dati_negativi)

# Visualizzare le distribuzioni
plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)
sns.histplot(dati_positivi, kde=True, color='blue')
plt.title(f'Skewness positiva: {skewness_positiva:.2f}')

plt.subplot(1, 2, 2)
sns.histplot(dati_negativi, kde=True, color='orange')
plt.title(f'Skewness negativa: {skewness_negativa:.2f}')

plt.show()

In questo esempio, sto creando due insiemi di dati, uno con una skewness positiva e uno con una skewness negativa. Sto usando una distribuzione esponenziale per il primo e una distribuzione beta per il secondo. Successivamente, calcolo la skewness per ciascun insieme di dati e visualizzo le distribuzioni utilizzando il modulo seaborn. La skewness viene poi stampata nel titolo di ciascun grafico.

Puoi eseguire questo codice nel tuo ambiente Python per vedere visivamente come la skewness riflette l’asimmetria delle distribuzioni. La skewness positiva è associata a una coda più lunga a destra, mentre la skewness negativa è associata a una coda più lunga a sinistra.

Libro Suggerito:

Se sei interessato all’argomento, ti suggerisco di leggere questo libro:

Practical Statistics for Data Scientists

Confronto tra diverse distribuzioni

Ecco un esempio di come puoi utilizzare Python per calcolare la skewness e confrontare la skewness tra diverse distribuzioni:

import numpy as np
from scipy.stats import skew
import matplotlib.pyplot as plt
import seaborn as sns

# Creare due insiemi di dati con skewness diversa
dati_set1 = np.random.normal(loc=0, scale=1, size=1000)
dati_set2 = np.random.exponential(scale=2, size=1000)

# Calcolare la skewness per entrambi gli insiemi di dati
skewness_set1 = skew(dati_set1)
skewness_set2 = skew(dati_set2)

# Visualizzare le distribuzioni
plt.figure(figsize=(12, 4))

plt.subplot(1, 2, 1)
sns.histplot(dati_set1, kde=True, color='blue')
plt.title(f'Skewness: {skewness_set1:.2f}')

plt.subplot(1, 2, 2)
sns.histplot(dati_set2, kde=True, color='orange')
plt.title(f'Skewness: {skewness_set2:.2f}')

plt.show()

# Stampare la skewness per confronto
print(f"Skewness del primo set di dati: {skewness_set1:.2f}")
print(f"Skewness del secondo set di dati: {skewness_set2:.2f}")

In questo esempio, sto generando due insiemi di dati con distribuzioni diverse: uno normale e uno esponenziale. Successivamente, calcolo la skewness per ciascun insieme di dati e visualizzo le distribuzioni usando il modulo seaborn. Infine, stampo la skewness per confrontare numericamente le asimmetrie delle distribuzioni.

Puoi eseguire questo codice nel tuo ambiente Python per vedere come la skewness riflette le differenze nella forma delle distribuzioni tra i due set di dati.

Libro consigliato:

Se ti piace quest’argomento, ti consiglio questo libro:

Fondamenti di Statistica per Data Scientists

Skewness nel rilevare anomalie di dati (Outliers)

La skewness di per sé non è generalmente utilizzata come strumento specifico per rilevare anomalie nei dati. Tuttavia, la skewness può essere una parte di un processo più ampio di identificazione di outlier o anomalie. Vediamo un esempio di come potresti utilizzare la skewness insieme ad altri metodi per rilevare anomalie utilizzando Python:

import numpy as np
from scipy.stats import skew
from sklearn.ensemble import IsolationForest
import matplotlib.pyplot as plt

# Creare un insieme di dati con un outlier
dati = np.concatenate([np.random.normal(0, 1, 1000), [10]])

# Calcolare la skewness
skewness = skew(dati)

# Utilizzare Isolation Forest per rilevare gli outlier
modello_isolation_forest = IsolationForest(contamination=0.01)  # Specificare la percentuale di contaminazione
dati = dati.reshape(-1, 1)  # Isolation Forest richiede un array 2D
modello_isolation_forest.fit(dati)

# Prevedere gli outlier
predizioni = modello_isolation_forest.predict(dati)

# Visualizzare i risultati
plt.scatter(range(len(dati)), dati, c=predizioni, cmap='viridis')
plt.xlabel('Indice dei dati')
plt.ylabel('Valore dei dati')
plt.title('Rilevamento di anomalie con Isolation Forest')
plt.show()

# Stampare la skewness e gli outlier
print("Skewness:", skewness)
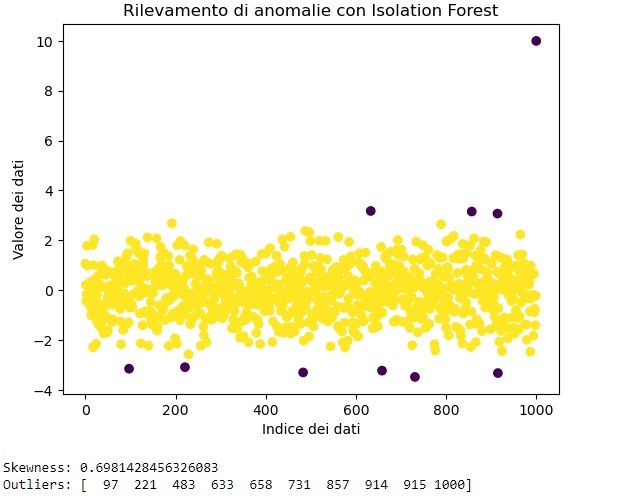
print("Outliers:", np.where(predizioni == -1)[0])

In questo esempio, stiamo generando un set di dati con una distribuzione normale e aggiungendo un outlier. Successivamente, calcoliamo la skewness e utilizziamo l’Isolation Forest per rilevare gli outlier. Infine, visualizziamo i dati con gli outlier identificati.

La skewness viene utilizzata qui più come una misura descrittiva, mentre l’Isolation Forest è utilizzato per rilevare gli outlier effettivi.