Algoritmi per la generazione dei numeri primi

Post Views: 337

La generazione di numeri primi è un argomento interessante in teoria dei numeri e ha diverse applicazioni in informatica, crittografia e altre discipline. Ci sono vari algoritmi per generare numeri primi in Python, e uno dei più comuni è l’algoritmo del crivello di Eratostene.

[wpda_org_chart tree_id=42 theme_id=50]

Il Crivello di Erastotene

L’algoritmo del crivello di Eratostene è un metodo efficiente per trovare tutti i numeri primi fino a un certo limite. Ecco un’implementazione di base in Python:

def eratosthenes_sieve(limit):
    primes = [True] * (limit + 1)
    
    # 0 and 1 are not prime
    primes[0] = primes[1] = False
    
    for number in range(2, int(limit**0.5) + 1):
        if primes[number]:
            # Set multiples of the current number to False
            primes[number**2 : limit + 1 : number] = [False] * len(primes[number**2 : limit + 1 : number])
    
    # Return the prime numbers
    return [number for number in range(2, limit + 1) if primes[number]]

# Example usage
upper_limit = 50
primes_up_to_limit = eratosthenes_sieve(upper_limit)
print(primes_up_to_limit)

Eseguendo si ottiene il seguente risultato:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

L’algoritmo del crivello di Eratostene inizia con un elenco di numeri da 2 a n, considera il primo numero (2) come primo, e poi elimina tutti i suoi multipli. Successivamente, passa al prossimo numero ancora segnato come primo e continua il processo.

Il crivello di Eratostene ha una complessità temporale asintotica di $O(n log log n)$ , dove $n$ è il limite superiore dei numeri primi che stai cercando di generare. Questa complessità è molto efficiente rispetto ad altri metodi per la generazione di numeri primi e rende il crivello di Eratostene una scelta pratica per la maggior parte degli scopi. La complessità $O(n log log n)$ deriva dalla sua capacità di eliminare i multipli di ciascun numero primo in modo efficiente, riducendo il numero complessivo di iterazioni necessarie.

Il Crivello di Atkins ed il Crivello Lineare di Sorenson

Esistono altri algoritmi più efficienti del crivello di Eratostene per la generazione di numeri primi in determinati contesti. Due esempi noti sono l’algoritmo di generazione di numeri primi di Atkins e il crivello lineare di Sorenson.

Crivello di Atkins

L’algoritmo di Atkins utilizza una combinazione di moduli aritmetici e pattern di selezione specifici per identificare i numeri primi. Ha una complessità asintotica di $O(n / log log n)$ , il che lo rende più veloce di Eratostene per alcune dimensioni di input.

def atkins_sieve(limit):
    is_prime = [False] * (limit + 1)
    sqrt_limit = int(limit**0.5) + 1

    for x in range(1, sqrt_limit):
        for y in range(1, sqrt_limit):
            n = 4 * x**2 + y**2
            if n <= limit and (n % 12 == 1 or n % 12 == 5):
                is_prime[n] = not is_prime[n]

            n = 3 * x**2 + y**2
            if n <= limit and n % 12 == 7:
                is_prime[n] = not is_prime[n]

            n = 3 * x**2 - y**2
            if x > y and n <= limit and n % 12 == 11:
                is_prime[n] = not is_prime[n]

    for n in range(5, sqrt_limit):
        if is_prime[n]:
            for k in range(n**2, limit + 1, n**2):
                is_prime[k] = False

    primes = [2, 3]
    primes.extend([num for num in range(5, limit + 1) if is_prime[num]])
    return primes

# Esempio di utilizzo
limit_superiore_atkins = 50
primi_atkins = atkins_sieve(limit_superiore_atkins)
print(primi_atkins)

Eseguendo si ottiene il medesimo risultato ottenuto in precedenza:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

Crivello Lineare di Sorenson

Il crivello lineare di Sorenson è un algoritmo più recente che ha dimostrato di essere efficiente per la generazione di numeri primi su intervalli specifici. Ha una complessità asintotica di $O(n / log n)$ ed è particolarmente utile quando è necessario generare primi su intervalli consecutivi.

def linear_sorenson_sieve(limit):
    is_prime = [True] * (limit + 1)
    primes = []

    for num in range(2, limit + 1):
        if is_prime[num]:
            primes.append(num)

        for prime in primes:
            if num * prime > limit:
                break
            is_prime[num * prime] = False

            if num % prime == 0:
                break

    return primes

# Esempio di utilizzo
limit_superiore_sorenson = 50
primi_sorenson = linear_sorenson_sieve(limit_superiore_sorenson)
print(primi_sorenson)

Eseguendo si ottiene il medesimo risultato ottenuto in precedenza:

[2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47]

È importante notare che la scelta dell’algoritmo dipende dal contesto specifico e dalle dimensioni degli input. Il crivello di Eratostene rimane una scelta solida e efficiente per molti casi, ma esplorare algoritmi alternativi può essere utile in situazioni in cui si richiede una maggiore ottimizzazione per dimensioni particolari.

Entrambi gli algoritmi hanno diverse peculiarità e ottimizzazioni specifiche. L’efficienza dipenderà dal contesto specifico in cui vengono utilizzati.

Paragoniamo i tre algoritmi tra di loro

Vediamo con un esempio pratico come si comportano in termini di efficienza i tre algoritmi appena definiti. Scriviamo un codice di prova come quello di seguito riportato:

import time
import matplotlib.pyplot as plt

def time_algorithm(algorithm, limit):
    start_time = time.time()
    algorithm(limit)
    return time.time() - start_time

def eratosthenes_sieve(limit):
    # Implementazione del crivello di Eratostene

def atkins_sieve(limit):
    # Implementazione del crivello di Atkins

def linear_sorenson_sieve(limit):
    # Implementazione del crivello lineare di Sorenson

# Valori di input
limits = [1000, 5000, 10000, 20000]

# Misura i tempi di esecuzione per ciascun algoritmo a diversi limiti
eratosthenes_times = [time_algorithm(eratosthenes_sieve, limit) for limit in limits]
atkins_times = [time_algorithm(atkins_sieve, limit) for limit in limits]
sorenson_times = [time_algorithm(linear_sorenson_sieve, limit) for limit in limits]

# Crea il grafico
plt.plot(limits, eratosthenes_times, label='Eratosthenes')
plt.plot(limits, atkins_times, label='Atkins')
plt.plot(limits, sorenson_times, label='Sorenson')

# Aggiungi etichette e legenda
plt.xlabel('Upper Limit')
plt.ylabel('Execution Time (s)')
plt.legend()

# Mostra il grafico
plt.show()

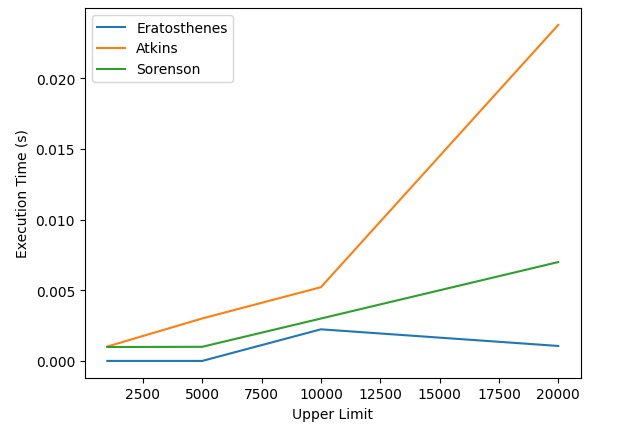
Eseguendo il codice si otterrà il grafico seguente che mostra il tempo di esecuzione dei diversi algoritmi per elaborare via via un numero sempre crescente di numeri primi

Metodi Probabilistici per la generazione di numeri primi

I metodi probabilistici per la generazione dei numeri primi coinvolgono l’uso di algoritmi che forniscono risultati probabilmente corretti, ma con una minima probabilità di errore. Questi algoritmi sono spesso preferiti in situazioni in cui la probabilità di ottenere un risultato errato può essere resa estremamente bassa attraverso iterazioni ripetute, e la loro efficienza può essere un vantaggio in confronto ai metodi deterministici.

Ecco alcuni metodi probabilistici per la generazione dei numeri primi:

Test di Primalità di Miller-Rabin: il test di primalità di Miller-Rabin è un algoritmo probabilistico ampiamente utilizzato. È basato sulla proprietà che se un numero composto viene testato come “probabilmente primo”, è estremamente improbabile che sia in realtà composto. Il test può essere ripetuto più volte per ridurre ulteriormente la probabilità di errore.
Generazione di Numeri Casuali: Un metodo semplice per generare numeri primi è generare casualmente un numero, verificare se è dispari, e poi utilizzare un test di primalità probabilistico come Miller-Rabin per determinare se è primo. Questo processo può essere ripetuto finché non viene trovato un numero primo.
Approcci basati su Curve Ellittiche: Alcuni algoritmi utilizzano curve ellittiche per generare numeri primi. Ad esempio, il “random walk” su una curva ellittica può essere utilizzato per generare numeri primi probabilisticamente.
Test di Primalità di Solovay-Strassen: Questo è un altro test probabilistico che può essere utilizzato per determinare la primalità di un numero. Funziona confrontando le proprietà del simbolo di Jacobi con la teoria dei numeri.
Test di primalità di Baillie-Pomerance-Selfridge-Wagstaff (BPSW): è un altro esempio di un test probabilistico di primalità. Esso è noto per essere probabilmente corretto e ha dimostrato di funzionare bene in pratica, ma è ancora basato su assunzioni non dimostrate. Il test di BPSW è spesso utilizzato in combinazione con altri test per fornire un livello aggiuntivo di fiducia nella primalità di un numero, soprattutto quando sono coinvolti numeri di grandi dimensioni utilizzati in contesti crittografici.

È importante notare che questi metodi probabilistici non garantiscono la primalità con certezza, ma la probabilità di errore può essere resa estremamente piccola con un numero sufficiente di iterazioni o attraverso determinate configurazioni. L’adattabilità e l’efficienza di questi algoritmi li rendono adatti per molte applicazioni, inclusi sistemi crittografici dove i numeri primi sono utilizzati per chiavi crittografiche.

Test di Primalità di Miller-Rabin

Vediamo come esempio il codice per il testi di Primalità di Miller Rabin

import random

def is_probably_prime(n, k=5):
    if n <= 1:
        return False
    if n <= 3:
        return True
    if n % 2 == 0:
        return False

    # Trova r e s tali che n - 1 = 2^r * s
    r, s = 0, n - 1
    while s % 2 == 0:
        r += 1
        s //= 2

    # Esegui k iterazioni del test
    for _ in range(k):
        a = random.randint(2, n - 2)
        x = pow(a, s, n)  # Calcolo di a^s mod n

        if x == 1 or x == n - 1:
            continue

        for _ in range(r - 1):
            x = pow(x, 2, n)
            if x == n - 1:
                break
        else:
            return False  # n è composto

    return True  # n è probabilmente primo

# Esempio di utilizzo
numero_da_testare = 23
ripetizioni_del_test = 5
risultato = is_probably_prime(numero_da_testare, ripetizioni_del_test)
print(f"{numero_da_testare} è probabilmente primo: {risultato}")

In questo esempio, la funzione is_probably_prime prende un numero intero n e un parametro opzionale k che rappresenta il numero di iterazioni del test di Miller-Rabin. Più iterazioni riducono la probabilità di errore, ma aumentano il tempo di esecuzione.