L’algoritmo di Kruskal è un algoritmo di tipo greedy utilizzato per trovare un Minimum Spanning Tree (MST) in un grafo con pesi sugli archi. Un Minimum Spanning Tree(MST) di un grafo è un sottoinsieme degli archi che connette tutti i nodi del grafo in modo che la somma dei pesi degli archi sia minima.
[wpda_org_chart tree_id=42 theme_id=50]
L’algoritmo di Kruscal
L’algoritmo di Kruskal è stato proposto da Joseph Kruskal nel 1956. Joseph Kruskal è un matematico e informatico americano, noto per i suoi contributi nel campo degli algoritmi, della teoria dei grafi e delle reti di computer. L’algoritmo è stato presentato in un articolo intitolato “On the Shortest Spanning Subtree of a Graph and the Traveling Salesman Problem” pubblicato sulla rivista Proceedings of the American Mathematical Society.
L’algoritmo di Kruskal è un algoritmo greedy che si basa sulla selezione degli archi del grafo in ordine crescente rispetto ai pesi. L’obiettivo è costruire un albero di copertura minimo attraverso la selezione degli archi in modo tale che non si formino cicli. L’algoritmo utilizza la struttura dati Union-Find (o Disjoint Set) per gestire le componenti connesse del grafo e per evitare la formazione di cicli durante la costruzione dell’albero.
L’algoritmo di Kruskal non è spesso espresso attraverso equazioni matematiche formali, ma piuttosto attraverso una descrizione algoritmica. La sua logica si basa su ordinamenti di archi e la gestione delle componenti connesse tramite operazioni di unione e ricerca. L’algoritmo di Kruskal utilizza una strategia greedy che seleziona gli archi in ordine crescente rispetto ai pesi, rendendolo più efficiente rispetto a un approccio puramente “forza bruta”.
Ecco una panoramica del funzionamento dell’algoritmo di Kruskal:
- Inizializzazione: Ordina gli archi del grafo in ordine crescente rispetto ai pesi.
- Inizializza l’albero: Inizia con un grafo che consiste solo nei nodi originali e nessun arco.
- Itera sugli archi: Inizia ad aggiungere gli archi al grafo, partendo da quelli con i pesi più bassi. Assicurati che l’aggiunta di un arco non crei un ciclo nel grafo corrente.
- Cicli e Union-Find: Per evitare la formazione di cicli, l’algoritmo utilizza una struttura dati chiamata Union-Find (o Disjoint Set) per tenere traccia delle componenti connesse del grafo. Prima di aggiungere un arco, controlla se i nodi di tale arco appartengono alla stessa componente con Union-Find. Se non appartengono alla stessa componente, aggiungi l’arco e unisci le due componenti.
- Terminazione: Continua ad aggiungere archi fino a quando tutti i nodi sono connessi o fino a quando tutti gli archi sono esauriti.
L’algoritmo di Kruskal è efficiente e ha una complessità temporale di ![]() , dove E è il numero di archi del grafo. È una scelta comune quando si cerca un algoritmo di MST in un grafo sparso o quando si devono gestire grafi di grandi dimensioni.
, dove E è il numero di archi del grafo. È una scelta comune quando si cerca un algoritmo di MST in un grafo sparso o quando si devono gestire grafi di grandi dimensioni.
Esistono altre alternative per trovare un Minimum Spanning Tree, come l’algoritmo di Prim. L’algoritmo di Prim utilizza un approccio simile, ma seleziona gli archi in base ai pesi minimi di nodi, piuttosto che ordinare tutti gli archi inizialmente. La scelta tra Kruskal e Prim dipende spesso dalla struttura del grafo e dai requisiti specifici dell’applicazione. Alcune ottimizzazioni, come l’uso di heap binari per l’ordinamento degli archi, possono essere applicate per migliorare ulteriormente le prestazioni dell’algoritmo di Kruskal.
I Grafi e la libreria Networkx
L’algoritmo di Kruskal può essere utilizzato su grafi non diretti e non pesati. In particolare, è adatto per grafi non orientati (ogni arco ha la stessa importanza indipendentemente dalla direzione) e pesati (ogni arco ha un peso associato). Il grafo può essere connesso o non connesso, ma la sua applicazione è più comune sui grafi connessi, poiché cerca di trovare un albero di copertura che connetta tutti i nodi.
Ora, procediamo con la rappresentazione grafica del grafo utilizzando la libreria networkx in Python:
import networkx as nx
import matplotlib.pyplot as plt
# Grafo di esempio con 7 elementi
graph = {
'A': [('B', 2), ('C', 1), ('D', 4)],
'B': [('A', 2), ('C', 3), ('D', 2)],
'C': [('A', 1), ('B', 3), ('D', 5)],
'D': [('A', 4), ('B', 2), ('C', 5)],
'E': [('D', 1)],
'F': [('A', 2), ('C', 4)],
'G': [('D', 3), ('F', 1)]
}
# Creazione del grafo di networkx
G = nx.Graph()
# Aggiungi nodi e archi al grafo di networkx
for node in graph:
G.add_node(node)
for neighbor, weight in graph[node]:
G.add_edge(node, neighbor, weight=weight)
# Posiziona i nodi con un algoritmo di layout
pos = nx.spring_layout(G)
# Disegna il grafo
nx.draw(G, pos, with_labels=True, font_weight='bold', node_size=700, node_color='skyblue')
# Etichetta i pesi degli archi
labels = {(edge[0], edge[1]): edge[2]['weight'] for edge in G.edges(data=True)}
nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)
plt.title("Example Graph with 7 Elements")
plt.show()
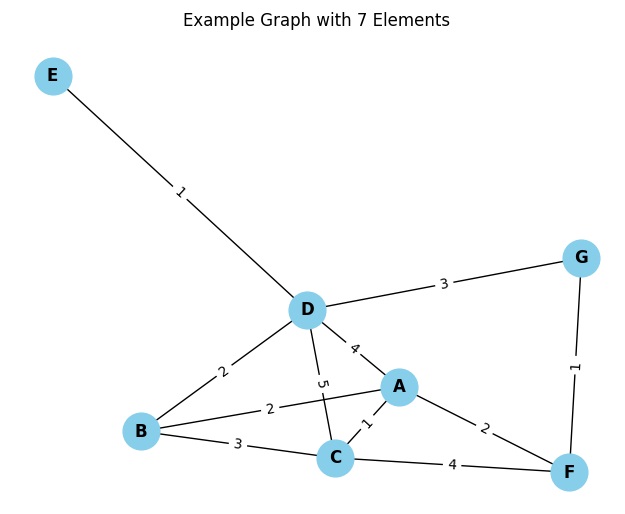
In questo codice, stiamo utilizzando la libreria networkx per creare il grafo e matplotlib per la visualizzazione. La funzione nx.Graph() crea un nuovo grafo vuoto, e poi attraverso un ciclo for, aggiungiamo nodi e archi al grafo di networkx. Infine, utilizziamo nx.draw() per disegnare il grafo con etichette dei nodi e nx.draw_networkx_edge_labels() per aggiungere etichette ai pesi degli archi. La funzione plt.show() visualizza il grafo.
Eseguendo si ottiene la rappresentazione grafica del grafo in questione.
MST (Minimum Spanning Tree)
MST (Minimum Spanning Tree), che tradotto in italiano significa “Albero di Copertura Minimo”. Un MST di un grafo non orientato e pesato è un sottoinsieme degli archi che collega tutti i nodi del grafo senza formare cicli e ha il peso totale più basso possibile. In altre parole, è un albero che connette tutti i nodi di un grafo con il minimo costo possibile.
Alcuni concetti chiave associati a un MST sono:
- Albero di Copertura: Un albero di copertura di un grafo è un sottoinsieme di archi che forma un albero e che tocca tutti i nodi del grafo.
- Pesatura: Ogni arco in un grafo pesato ha un valore associato chiamato “peso”. L’obiettivo è trovare un sottoinsieme di archi il cui peso totale è minimo.
L’MST è utilizzato in vari contesti, tra cui:
- Reti di Comunicazione: In reti di telecomunicazioni o computer, l’MST può essere utilizzato per la progettazione di reti di connessione a basso costo tra vari punti.
- Progettazione di Circuiti Elettrici: Nella progettazione di circuiti elettrici, l’MST può rappresentare una connessione a basso costo tra vari componenti.
- Routing di Reti: Nella progettazione di reti di computer o di trasporto dati, l’MST può essere utilizzato per determinare percorsi di trasmissione a costo minimo.
- Clusterizzazione di Dati: In analisi di dati o apprendimento automatico, l’MST può essere utilizzato per identificare relazioni e connessioni significative tra i dati.
L’MST è un concetto fondamentale in teoria dei grafi e fornisce una soluzione ottimale per problemi di connessione a costo minimo in molte applicazioni pratiche. Gli algoritmi come l’algoritmo di Kruskal o l’algoritmo di Prim sono spesso utilizzati per trovare l’MST di un grafo.
Applicazione dell’algoritmo di Kruskal
Ecco una versione del codice che applica l’algoritmo di Kruskal al grafo di esempio e fornisce una rappresentazione grafica:
import networkx as nx
import matplotlib.pyplot as plt
def find_mst_kruskal(graph):
edges = []
for node in graph:
for neighbor, weight in graph[node]:
edges.append((node, neighbor, weight))
edges.sort(key=lambda x: x[2])
mst_edges = []
parent = {node: node for node in graph}
def find(node):
if parent[node] != node:
parent[node] = find(parent[node])
return parent[node]
def union(node1, node2):
root1 = find(node1)
root2 = find(node2)
parent[root1] = root2
for edge in edges:
node1, node2, weight = edge
if find(node1) != find(node2):
mst_edges.append(edge)
union(node1, node2)
return mst_edges
# Grafo di esempio con 7 elementi
graph = {
'A': [('B', 2), ('C', 1), ('D', 4)],
'B': [('A', 2), ('C', 3), ('D', 2)],
'C': [('A', 1), ('B', 3), ('D', 5)],
'D': [('A', 4), ('B', 2), ('C', 5)],
'E': [('D', 1)],
'F': [('A', 2), ('C', 4)],
'G': [('D', 3), ('F', 1)]
}
# Applica l'algoritmo di Kruskal
minimum_spanning_tree = find_mst_kruskal(graph)
print("Minimum Spanning Tree:", minimum_spanning_tree)
# Creazione del grafo di networkx
G = nx.Graph()
# Aggiungi nodi e archi al grafo di networkx
for node in graph:
G.add_node(node)
for neighbor, weight in graph[node]:
G.add_edge(node, neighbor, weight=weight)
# Posiziona i nodi con un algoritmo di layout
pos = nx.spring_layout(G)
# Disegna il grafo originale
plt.figure(figsize=(12, 6))
plt.subplot(121)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_size=700, node_color='skyblue')
plt.title("Original Graph")
# Disegna l'MST
plt.subplot(122)
nx.draw(G, pos, with_labels=True, font_weight='bold', node_size=700, node_color='skyblue')
nx.draw_networkx_edges(G, pos, edgelist=minimum_spanning_tree, edge_color='red', width=2)
plt.title("Minimum Spanning Tree")
plt.show()Spiegazione delle parti principali del codice:
find_mst_kruskal: Questa funzione implementa l’algoritmo di Kruskal per trovare il Minimum Spanning Tree. Utilizza la struttura dati Union-Find per gestire le componenti connesse del grafo.- Applicazione dell’algoritmo a un grafo di esempio: Viene creato un grafo di esempio con 7 elementi e l’algoritmo di Kruskal viene applicato ad esso per trovare l’MST.
- Creazione del grafo di networkx e rappresentazione grafica:
- Viene creato un grafo di networkx e gli archi vengono aggiunti con i rispettivi pesi.
- La funzione
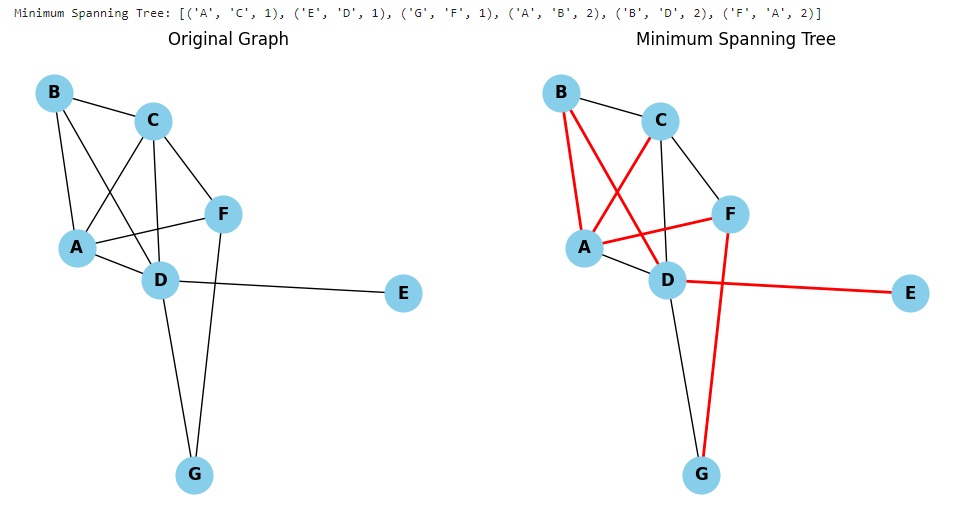
nx.spring_layoutè utilizzata per posizionare i nodi con un algoritmo di layout. - La rappresentazione grafica del grafo originale e dell’MST risultante viene mostrata in due subplot separati. Gli archi dell’MST sono evidenziati in rosso.
Eseguendo il codice si ottiene:
Conclusioni
In conclusione, l’algoritmo di Kruskal e i concetti associati all’MST sono fondamentali nella teoria dei grafi e hanno numerose applicazioni pratiche, soprattutto quando si tratta di connessioni a costo minimo in vari domini. La rappresentazione grafica dei grafi è un prezioso strumento per comprendere visivamente le relazioni e le strutture nei dati.