La kurtosis è una misura statistica che descrive la forma della distribuzione di un insieme di dati. Essenzialmente, indica quanto le code di una distribuzione differiscono da quelle di una distribuzione normale. Un valore di kurtosis superiore a zero suggerisce code più pesanti (distribuzione più “appuntita”), mentre un valore inferiore indica code più leggere (distribuzione più “piatta”). La kurtosis può essere positiva (le code sono più pesanti), negativa (le code sono più leggere) o zero (simile a una distribuzione normale).
[wpda_org_chart tree_id=15 theme_id=50]
Kurtosis
La kurtosis di una distribuzione può essere calcolata utilizzando la seguente formula:
![]()
dove:
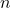 è il numero di osservazioni nella distribuzione,
è il numero di osservazioni nella distribuzione,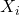 sono le singole osservazioni,
sono le singole osservazioni,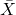 è la media della distribuzione.
è la media della distribuzione.
Questo calcolo fornisce un valore numerico che rappresenta la kurtosis della distribuzione dei dati. Un risultato di 3 indica una distribuzione normale, mentre valori superiori a 3 indicano code più pesanti (distribuzione più “appuntita”) e valori inferiori indicano code più leggere (distribuzione più “piatta”).
Il calcolo della kurtosis nell’analisi dei dati fornisce informazioni sulla forma della distribuzione dei dati. Questa misura è utile per comprendere la tendenza dei dati ad avere code più pesanti o più leggere rispetto a una distribuzione normale.
- Forma della distribuzione: La kurtosis aiuta a identificare se la distribuzione dei dati è più “appuntita” (kurtosis positiva) o più “piatta” (kurtosis negativa) rispetto a una distribuzione normale.
- Outliers: Un alto valore di kurtosis può indicare la presenza di outliers o estremi nella distribuzione. Questo può essere importante per riconoscere eventuali punti anomali nei dati.
- Decisioni statistiche: La kurtosis può influenzare le decisioni statistiche. Ad esempio, in alcuni test statistici, l’assunzione di normalità della distribuzione può essere importante, e la kurtosis può aiutare a valutare questa normalità.
In sintesi, la kurtosis fornisce una misura della “pesantezza” delle code della distribuzione, contribuendo a una comprensione più approfondita della struttura dei dati e supportando decisioni analitiche o di modellazione.
In termini più discorsivi, la kurtosis, considerata insieme ad altre statistiche descrittive e strumenti di analisi dati, offre un’opportunità di esplorare la forma complessiva di una distribuzione. Questo aspetto è cruciale perché, mentre la media e la deviazione standard ci forniscono informazioni sulla posizione e la dispersione centrale dei dati, la kurtosis va oltre, aiutandoci a capire quanto siano comuni o rari gli eventi estremi. Questa capacità di rivelare la presenza di code più pesanti o più leggere nella distribuzione è particolarmente utile in situazioni dove la comprensione della variabilità e l’identificazione di dati outlier sono cruciali, come nell’analisi finanziaria o nelle decisioni statistiche più complesse.

Libro Suggerito:
Se sei interessato all’argomento, ti suggerisco di leggere questo libro:
Esempio di calcolo di Kurtosis
Certamente! Puoi utilizzare la libreria scipy in Python per calcolare la kurtosis di un insieme di dati. Ecco un esempio di come farlo:
import numpy as np
from scipy.stats import kurtosis
# Genera un set di dati di esempio
dati = np.random.normal(size=1000)
# Calcola la kurtosis
kurtosis_value = kurtosis(dati)
print(f"Kurtosis del set di dati: {kurtosis_value}")Otterrai un risultato variabile (i dati sono generati casualmente) simile al seguente:
Kurtosis del set di dati: 0.02330805973832817In questo esempio, numpy viene utilizzato per generare un set di dati casuali con una distribuzione normale, e scipy.stats.kurtosis calcola la kurtosis di questi dati. Il risultato viene quindi stampato a schermo. Ricorda che il valore di kurtosis da solo potrebbe non essere molto interpretativo, ma andrebbe interpretato in relazione al contesto e alle aspettative della tua analisi dei dati.
Utilizzo del calcolo di Kurtosis ed esempi
Ecco alcuni punti chiave sulla kurtosis e sul suo utilizzo:
- Forma della distribuzione:
- Kurtosis positiva: Indica che le code della distribuzione sono più pesanti rispetto a una distribuzione normale. Ciò significa che ci sono più dati estremi.
- Kurtosis negativa: Indica che le code della distribuzione sono più leggere rispetto a una distribuzione normale. Ciò significa che ci sono meno dati estremi.
- Confronto con la distribuzione normale:
- Una distribuzione normale ha una kurtosis di 3. Un valore superiore a 3 indica code più pesanti, mentre un valore inferiore indica code più leggere.
- Una distribuzione normale ha una kurtosis di 0 quando si utilizza la definizione “excess kurtosis,” che sottrae 3 dal valore grezzo.
- Identificazione di outliers:
- Elevati valori di kurtosis possono indicare la presenza di outliers o estremi nella distribuzione. Questo può essere utile per l’identificazione di dati anomali.
- Decisioni statistiche:
- In alcune analisi statistiche, l’assunzione di normalità della distribuzione è importante. La kurtosis può aiutare a valutare se questa assunzione è valida.
- Modello di rischio finanziario:
- Nella finanza, la kurtosis può essere utilizzata per valutare il rischio di rendimenti finanziari, poiché code più pesanti indicano una maggiore probabilità di eventi estremi.
In generale, la kurtosis fornisce una panoramica sulla forma della distribuzione e può essere utile nella comprensione della variabilità e degli outlier nei dati, influenzando decisioni statistiche e modellazione. Va notato che la kurtosis da sola potrebbe non essere sufficiente per trarre conclusioni definitive, ed è spesso considerata insieme ad altre statistiche descrittive e tecniche di analisi dati.
Esempio di analisi sulla forma delle distribuzioni
Certamente! Utilizzeremo la libreria matplotlib per visualizzare le distribuzioni dei dati e scipy.stats per calcolare la kurtosis. Assicurati di avere installate entrambe le librerie eseguendo:
pip install matplotlib scipyEcco un esempio di analisi delle forme delle distribuzioni:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import kurtosis, skew, norm
# Genera dati da una distribuzione normale
dati_normale = np.random.normal(size=1000)
# Genera dati da una distribuzione con code più pesanti (kurtosis positiva)
dati_pesanti = np.random.standard_t(df=5, size=1000)
# Genera dati da una distribuzione con code più leggere (kurtosis negativa)
dati_leggeri = np.random.uniform(size=1000)
# Funzione per mostrare la distribuzione e calcolare kurtosis e skewness
def analizza_distribuzione(dati, titolo):
plt.figure(figsize=(10, 6))
# Visualizza l'istogramma dei dati
plt.hist(dati, bins=50, density=True, alpha=0.7, color='blue')
# Visualizza la funzione di densità di probabilità della distribuzione normale
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, np.mean(dati), np.std(dati))
plt.plot(x, p, 'k', linewidth=2)
# Calcola e stampa kurtosis e skewness
kurt = kurtosis(dati)
skewness = skew(dati)
plt.title(f'{titolo}\nKurtosis: {kurt:.2f}, Skewness: {skewness:.2f}')
plt.show()
# Analizza le tre distribuzioni
analizza_distribuzione(dati_normale, 'Distribuzione Normale')
analizza_distribuzione(dati_pesanti, 'Distribuzione con Kurtosis Positiva')
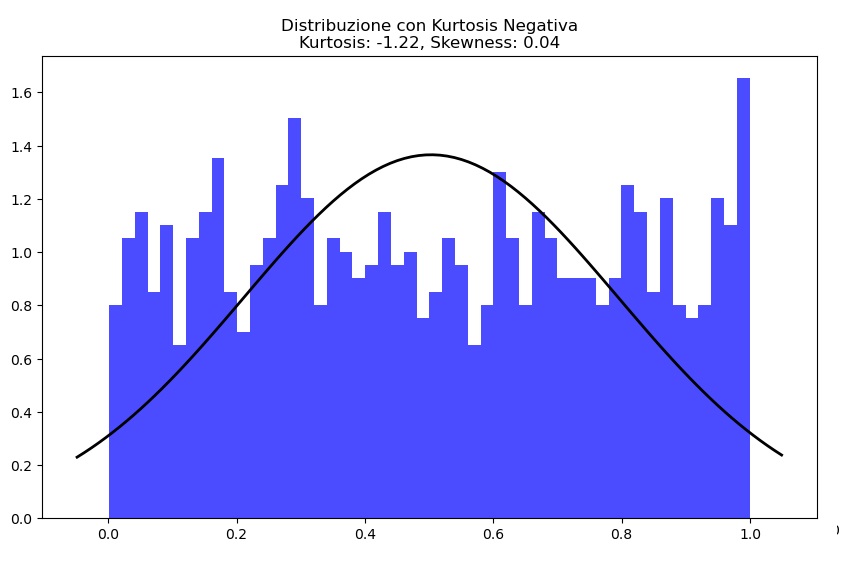
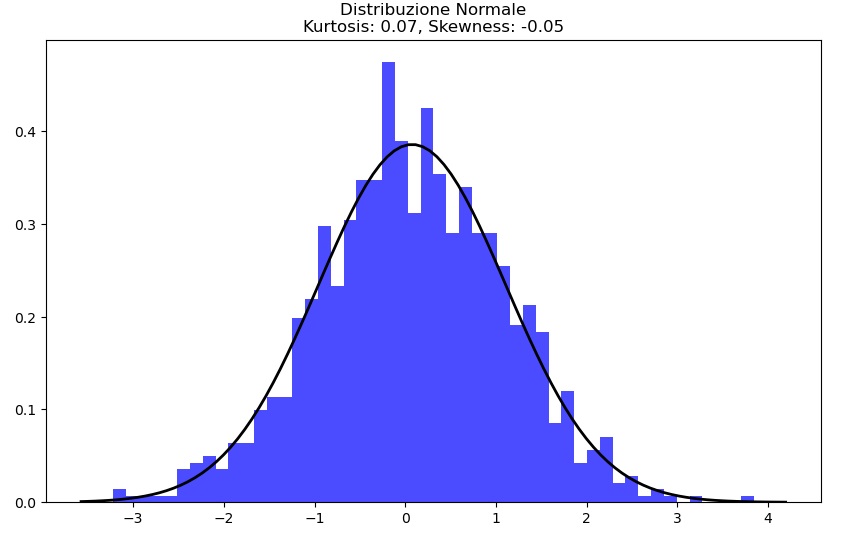
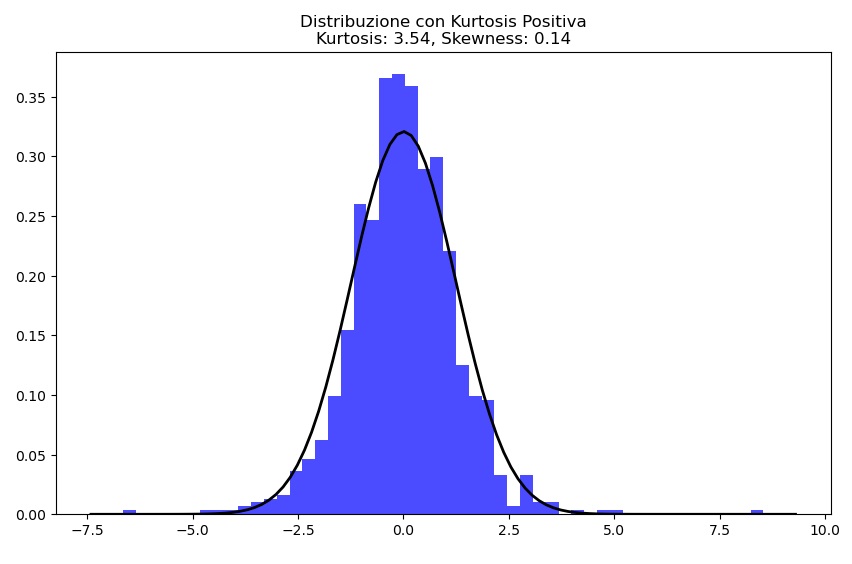
analizza_distribuzione(dati_leggeri, 'Distribuzione con Kurtosis Negativa')In questo esempio, stiamo generando tre insiemi di dati: uno da una distribuzione normale, uno con code più pesanti (t-distribution con gradi di libertà bassi), e uno con code più leggere (distribuzione uniforme). La funzione analizza_distribuzione visualizza l’istogramma dei dati, sovrappone la funzione di densità di probabilità della distribuzione normale e calcola kurtosis e skewness, fornendo un’analisi visiva e numerica delle distribuzioni.
La prima è una distribuzione normale dato che ha il valore di Kurtosis prossima a zero.
La seconda distribuzione invece presenta un valore di kurtosis positivo e quindi i valori centrali della distribuzione risulteranno maggiori in numero rispetto ad una distribuzione normale.

Se vuoi approfondire l’argomento e scoprire di più sul mondo della Data Science con Python, ti consiglio di leggere il mio libro:
Fabio Nelli
La terza distribuzione invece presenta un valore di kurtosis negativo e quindi i valori saranno maggiormente distribuiti su tutto il range della distribuzione con un conseguente allargamento delle code rispetto ad una distribuzione normale. Con valori sempre più alti si tenderà ad una distribuzione uniforme.