Nel vasto panorama degli algoritmi di risoluzione dei problemi, due approcci principali emergono come metodi distinti ma complementari: il Backtracking e la Forza Bruta. Entrambi sono utilizzati per risolvere problemi computazionali attraverso la ricerca esaustiva delle soluzioni, ma le loro strategie differiscono in modo significativo.
In questo articolo, esamineremo diverse dimensioni dei due approcci, dalla complessità computazionale alla loro applicazione pratica. Attraverso esempi concreti e casi di studio, metteremo in evidenza le situazioni in cui il Backtracking eccelle rispetto alla Forza Bruta e viceversa. Sottolineeremo inoltre l’importanza di una corretta implementazione e considerazioni sulla complessità temporale.
[wpda_org_chart tree_id=42 theme_id=50]
Backtracking e Forza Bruta: due approcci a confronto
Backtracking: La Ricerca Intelligente
Il Backtracking è una strategia che si basa sulla ricerca esaustiva, ma con l’aggiunta di una componente intelligente. Esso esplora le possibilità in modo ricorsivo, facendo scelte e annullando tali scelte quando riconosce che una soluzione parziale non può portare a una soluzione completa. Questa tecnica è particolarmente adatta per problemi di decisione complessi, dove è possibile eliminare molte soluzioni non promettenti.
Forza Bruta: L’Approccio Diretto
Dall’altro lato dello spettro, la Forza Bruta è un approccio diretto ed esaustivo che esamina tutte le possibili soluzioni una dopo l’altra, senza strategie di pruning o eliminazione delle soluzioni non ottimali. Sebbene possa essere meno efficiente su problemi complessi, la Forza Bruta è spesso utilizzata quando la dimensione del problema è limitata o quando non è possibile applicare strategie di ottimizzazione.
Cos’è il Backtracking?
Il backtracking è una tecnica di risoluzione dei problemi che si basa sulla ricerca esaustiva di tutte le soluzioni possibili per un determinato problema. In sostanza, il backtracking esplora tutte le possibilità di una soluzione e, quando si rende conto che la soluzione parziale che sta esaminando non può portare a una soluzione completa, fa “backtrack” alla decisione precedente e riprende l’esplorazione da lì.
La tecnica del backtracking segue una struttura ricorsiva, e il suo pseudocodice può essere rappresentato in modo generale come segue:
def backtrack(soluzione_parciale, altri_parametri):
if soluzione_parciale è completa:
# Aggiungi soluzione_parciale alla lista delle soluzioni
else:
for scelta in scelte_possibili:
if scelta è valida:
# Fai una scelta
aggiorna soluzione_parciale
# Chiamata ricorsiva
backtrack(soluzione_parciale, altri_parametri)
# Annulla la scelta (backtrack)
ripristina soluzione_parcialeIl Problema delle N Regine
Questo approccio è particolarmente utile per risolvere problemi di decisione, come ad esempio il problema delle N regine, il problema del commesso viaggiatore e molti altri.
Implementiamo un esempio semplice di backtracking per risolvere il problema delle N regine. In questo problema, l’obiettivo è posizionare N regine su una scacchiera N x N in modo che nessuna regina minacci un’altra.
def is_safe(board, row, col, n):
# Verifica se è sicuro posizionare una regina in questa posizione
for i in range(row):
if board[i][col] == 1:
return False
if col - i >= 0 and board[row - i][col - i] == 1:
return False
if col + i < n and board[row - i][col + i] == 1:
return False
return True
def solve_n_queens_util(board, row, n, solutions):
if row == n:
# Abbiamo trovato una soluzione completa
solutions.append([row[:] for row in board])
return
for col in range(n):
if is_safe(board, row, col, n):
# Fai una scelta
board[row][col] = 1
# Chiamata ricorsiva
solve_n_queens_util(board, row + 1, n, solutions)
# Annulla la scelta (backtrack)
board[row][col] = 0
def solve_n_queens(n):
board = [[0] * n for _ in range(n)]
solutions = []
solve_n_queens_util(board, 0, n, solutions)
return solutions
# Esempio di utilizzo
n = 4
solutions = solve_n_queens(n)
for solution in solutions:
print(solution)In questo esempio, solve_n_queens restituirà una lista di tutte le possibili disposizioni delle N regine sulla scacchiera. La funzione is_safe verifica se è sicuro posizionare una regina in una determinata posizione. La funzione solve_n_queens_util è una funzione di supporto ricorsiva che esplora tutte le possibili soluzioni. Eseguendo si ottiene il seguente risultato:
[[0, 1, 0, 0], [0, 0, 1, 0], [1, 0, 0, 0], [0, 0, 0, 1]]
[[0, 1, 0, 0], [0, 0, 0, 1], [1, 0, 0, 0], [0, 0, 1, 0]]
[[0, 0, 1, 0], [1, 0, 0, 0], [0, 0, 0, 1], [0, 1, 0, 0]]
[[0, 0, 1, 0], [0, 1, 0, 0], [0, 0, 0, 1], [1, 0, 0, 0]]Questa è solo un’esempio di come il backtracking può essere utilizzato per risolvere un problema specifico. La chiave è adattare la struttura generale del backtracking al problema specifico che si sta affrontando.
Backtracking vs Forza Bruta
Il backtracking e la forza bruta sono due approcci risolvere problemi computazionali in maniera esaustiva, ma hanno differenze significative nel modo in cui affrontano la ricerca delle soluzioni.
Forza Bruta (Brute Force)
La forza bruta è un approccio diretto ed esaustivo per risolvere un problema, in cui tutte le possibili soluzioni vengono esaminate una dopo l’altra fino a trovare quella corretta. Questo approccio può essere inefficiente su problemi complessi, in quanto esamina tutte le combinazioni possibili, senza alcuna strategia di pruning o eliminazione delle soluzioni che non possono portare a una soluzione ottimale.
Ad esempio, considera un problema in cui devi trovare la somma massima di una sotto-sequenza in un array. La forza bruta esaminerebbe tutte le possibili sotto-sequenze e confronterebbe le somme, senza considerare alcuna proprietà strutturale del problema.
def max_subarray_sum_bruteforce(arr):
n = len(arr)
max_sum = float('-inf')
for i in range(n):
for j in range(i, n):
current_sum = sum(arr[i:j+1])
max_sum = max(max_sum, current_sum)
return max_sumQuesto approccio può essere inefficiente per problemi con grandi spazi di ricerca.
Backtracking
Il backtracking è un approccio basato sulla ricerca esaustiva delle soluzioni, ma con l’aggiunta di una strategia di pruning. Esso esplora le soluzioni in modo ricorsivo, effettuando delle scelte e verificando se conducono a una soluzione accettabile. Se si scopre che una particolare scelta non può portare a una soluzione valida, il backtracking fa “backtrack” e annulla la scelta, esplorando altre possibilità.
Nel paragrafo precedente, abbiamo visto un esempio di backtracking risolvendo il problema delle N regine. Questo approccio si concentra sulla generazione incrementale delle soluzioni, facendo scelte e annullando le scelte quando necessario.
Il backtracking è spesso più efficiente della forza bruta per problemi in cui esistono molte scelte possibili e alcune di esse possono essere eliminate in modo intelligente. Tuttavia, la complessità temporale può ancora essere elevata in determinati casi.
In conclusione, mentre la forza bruta esamina tutte le possibilità senza strategie di pruning, il backtracking aggiunge un livello di intelligenza alla ricerca esplorando solo le possibilità rilevanti, riducendo così il tempo computazionale. Entrambi gli approcci hanno i loro usi a seconda del problema specifico che si sta affrontando.
Il Problema del Commesso Viaggiatore
Per meglio vedere la differenza che c’è tra l’approccio Forza Bruta e la tecnica del Backtracking, applicheremo un esempio pratico: il problema del commesso viaggiatore (TSP – Travelling Salesman Problem), che coinvolge la ricerca del percorso più breve che attraversa tutti i punti dati esattamente una volta.
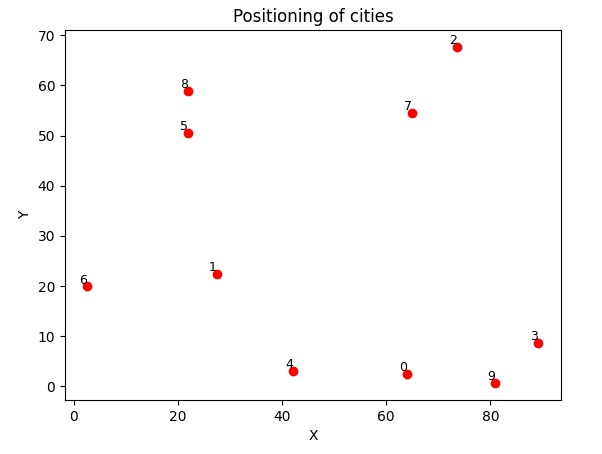
In questo esempio, implementeremo una soluzione di forza bruta e una soluzione di backtracking per risolvere il TSP. Successivamente, useremo la libreria matplotlib per visualizzare le differenze di efficienza tra i due approcci. Per prima cosa generiamo una serie di città disposte in maniera casuale in uno spazio di coordinate (X.Y).
import random
import matplotlib.pyplot as plt
def distance(city1, city2):
return ((city1[0] - city2[0]) ** 2 + (city1[1] - city2[1]) ** 2) ** 0.5
def plot_cities(cities):
x, y = zip(*cities)
plt.scatter(x, y, c='red', marker='o')
for i, (xi, yi) in enumerate(cities):
plt.text(xi, yi, str(i), fontsize=9, ha='right', va='bottom')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Positioning of cities')
plt.show()
# Generazione di città casuali per il test
def generate_random_cities(num_cities):
random.seed(42)
cities = [(random.uniform(0, 100), random.uniform(0, 100)) for _ in range(num_cities)]
return cities
# Visualizzazione delle città
num_cities = 10
cities = generate_random_cities(num_cities)
plot_cities(cities)Eseguendo otterremo la rappresentazione grafica delle città disposte su un piano cartesiano
Adesso risolviamo il problema del commesso viaggiatore utilizzando sia la forza bruta che il backtracking, e infine, mostreremo un grafico comparativo del tempo impiegato dai due approcci. I tempi possono variare a seconda della configurazione casuale delle città e della potenza computazionale del sistema in uso.
Il calcolo ci dovrà fornire come risultato il percorso più breve che il commesso viaggiatore dovrà fare per visitare tutte le città mostrate nel grafico sopra. Per tale calcolo applicheremo i due diversi approcci fornendo due diverse funzioni.
Forza Bruta (tsp_bruteforce)
def tsp_bruteforce(cities):
start_time = time.time()
shortest_path = None
shortest_distance = float('inf')
for perm in itertools.permutations(range(len(cities))):
current_distance = total_distance(perm, cities)
if current_distance < shortest_distance:
shortest_distance = current_distance
shortest_path = perm
elapsed_time = time.time() - start_time
return shortest_path, shortest_distance, elapsed_time- Inizializzazione: La funzione
tsp_bruteforceinizia misurando il tempo iniziale (start_time) e inizializza le variabilishortest_patheshortest_distanceper tenere traccia della soluzione più breve e della sua distanza. - Permutazioni: Utilizzando
itertools.permutations, vengono generate tutte le possibili permutazioni degli indici delle città. Ogni permutazione rappresenta un possibile percorso da esaminare. - Calcolo della Distanza: Per ogni permutazione, viene calcolata la distanza totale del percorso utilizzando la funzione
total_distance. - Aggiornamento della Soluzione Migliore: Se la distanza calcolata è inferiore alla distanza corrente della soluzione migliore (
shortest_distance), la soluzione migliore viene aggiornata. - Misurazione del Tempo: Alla fine del processo, viene calcolato il tempo totale impiegato.
Backtracking (tsp_backtracking)
def tsp_backtracking(cities):
start_time = time.time()
def backtrack(path):
if len(path) == len(cities):
nonlocal shortest_path, shortest_distance
current_distance = total_distance(path, cities)
if current_distance < shortest_distance:
shortest_distance = current_distance
shortest_path = path
else:
for i in range(len(cities)):
if i not in path:
backtrack(path + [i])
shortest_path = None
shortest_distance = float('inf')
backtrack([])
elapsed_time = time.time() - start_time
return shortest_path, shortest_distance, elapsed_time- Inizializzazione: La funzione
tsp_backtrackinginizia misurando il tempo iniziale (start_time) e inizializza le variabilishortest_patheshortest_distance. - Funzione di Backtrack Ricorsiva: La funzione
backtrackè una funzione ricorsiva che esplora tutte le possibili permutazioni dei percorsi. Se la lunghezza del percorso corrente è uguale al numero di città, viene calcolata la distanza totale e aggiornata la soluzione migliore se necessario. Altrimenti, per ogni città non ancora inclusa nel percorso, la funzione si richiama ricorsivamente aggiungendo la città al percorso. - Inizializzazione del Backtrack: La funzione principale
tsp_backtrackinginizia il processo di backtracking chiamandobacktrack([]), indicando che il percorso iniziale è vuoto. - Misurazione del Tempo: Alla fine del processo, viene calcolato il tempo totale impiegato.
Backtracking vs Brute Force
Adesso scriviamo il codice interamente che effettuerà il calcolo del percorso più breve con entrambe gli approcci e poi paragoneremo i risultati ottenuti ed il tempo impiegato.
import itertools
import time
import matplotlib.pyplot as plt
def total_distance(path, cities):
total_dist = 0
for i in range(len(path) - 1):
total_dist += distance(cities[path[i]], cities[path[i + 1]])
return total_dist
# Soluzione di Forza Bruta per il TSP
def tsp_bruteforce(cities):
start_time = time.time()
shortest_path = None
shortest_distance = float('inf')
for perm in itertools.permutations(range(len(cities))):
current_distance = total_distance(perm, cities)
if current_distance < shortest_distance:
shortest_distance = current_distance
shortest_path = perm
elapsed_time = time.time() - start_time
return shortest_path, shortest_distance, elapsed_time
# Soluzione di Backtracking per il TSP
def tsp_backtracking(cities):
start_time = time.time()
def backtrack(path):
if len(path) == len(cities):
nonlocal shortest_path, shortest_distance
current_distance = total_distance(path, cities)
if current_distance < shortest_distance:
shortest_distance = current_distance
shortest_path = path
else:
for i in range(len(cities)):
if i not in path:
backtrack(path + [i])
shortest_path = None
shortest_distance = float('inf')
backtrack([])
elapsed_time = time.time() - start_time
return shortest_path, shortest_distance, elapsed_time
# Esecuzione delle soluzioni
bruteforce_result = tsp_bruteforce(cities)
backtracking_result = tsp_backtracking(cities)
# Stampa dei risultati
print("Brute force:")
print("Shortest route:", bruteforce_result[0])
print("Minimum distance:", bruteforce_result[1])
print("Execution time (seconds):", bruteforce_result[2])
print("\nBacktracking:")
print("Shortest route:", backtracking_result[0])
print("Minimum distance:", backtracking_result[1])
print("Execution time (seconds):", backtracking_result[2])
# Creazione del grafico di confronto
labels = ['Brute force', 'Backtracking']
times = [bruteforce_result[2], backtracking_result[2]]
plt.bar(labels, times, color=['blue', 'green'])
plt.ylabel('Execution time (seconds)')
plt.title('Comparison between Brute Force and Backtracking for TSP')
plt.show()
L’esecuzione richiederà diversi secondi (quasi un minuto). Al termine del calcolo verranno visualizzati i seguenti risultati:
Brute force:
Shortest route: (2, 7, 8, 5, 6, 1, 4, 0, 9, 3)
Minimum distance: 203.1584418265072
Execution time (seconds): 23.648714065551758
Backtracking:
Shortest route: [2, 7, 8, 5, 6, 1, 4, 0, 9, 3]
Minimum distance: 203.1584418265072
Execution time (seconds): 27.852330446243286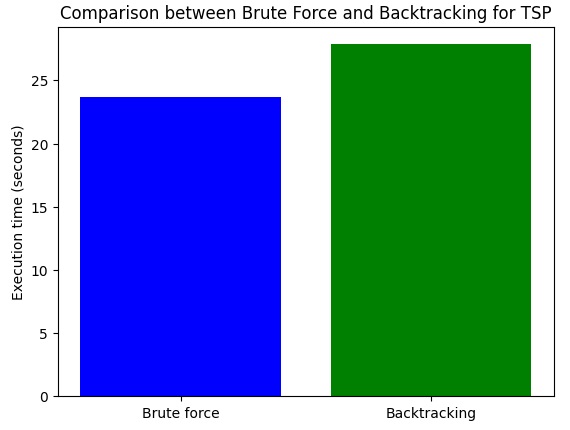
Interessante il risultato. In questo caso, l’approccio Brute Force risulterebbe più efficiente del Backtracking, impiegando per il calcolo alcuni secondi in meno.