Le rotazioni in 3D e gli angoli di Eulero in Python

Post Views: 25.435

Le realtà virtuali con cui spesso giochiamo sui nostri PC sono basate su motori 3D, cioè sistemi in grado di effettuare calcoli che simulino lo spostamento e la rotazione di oggetti in un sistema tridimensionale. Anche in robotica, in particolare con i bracci robotici, si fa uso di sistemi in grado di calcolare un determinato movimento, stabilendo di quanto dovranno ruotare i singoli motori che li compongono. Tutti questi sistemi si basano su calcoli e concetti matematici in grado di calcolare ogni singolo movimento nello spazio tridimensionale, di cui gran parte furono sviluppati dal famoso matematico Eulero (1707-1784). In questo articolo vedremo cosa sono gli angoli di Eulero, come si calcolano e come si può calcolare il moto di rotazione di un corpo rigido nello spazio euclideo a tre dimensioni. Il tutto con prove pratiche passo passo sviluppate in Python.

Le rotazioni in 3D e gli Angoli di Eulero con Python

Teorema di Eulero

“Ogni spostamento di un corpo rigido nello spazio tridimensionale, con un punto che rimane fisso, è equivalente ad una singola rotazione del corpo intorno ad un asse passante per il punto fisso”

Questo teorema fu formulato da Eulero nel 1775.

In altre parole, se consideriamo due sistemi di riferimento cartesiani, uno (X₀,Y₀,Z₀) e l’altro (X₁,Y₁,Z₁), che hanno lo stesso punto di origine O, ma diverso orientamento, esisterà sempre un unico asse di rotazione con il quale il primo sistema assumerà la stessa configurazione del secondo sistema.

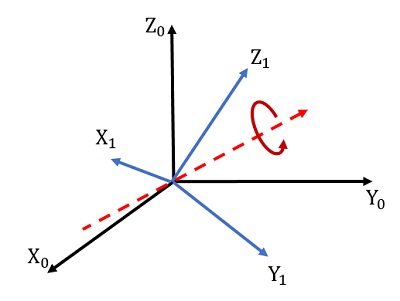
Angoli di Eulero - due sistemi di riferimento

In maniera ancora più semplice, qualsiasi rotazione può essere descritta mediante una sequenza di tre successive rotazioni, chiamate anche rotazioni elementari, che si effettuano intorno ad uno dei tre assi coordinati X,Y e Z

Le rotazioni elementari

Esistono quindi tre rotazioni elementari, ciascuna intorno al suo asse di riferimento cartesiano X,Y e Z. Ma la rotazione intorno ad un asse può avvenire in due versi opposti. Ma quale dei due è quello positivo?

La rotazione intorno ad un asse è positiva se risponde alla regola della mano destra. Per esempio nel caso della rotazione intorno all’asse z, la rotazione sarà positiva a seconda della disposizione degli assi X e Y nella rappresentazione.

Quindi il verso delle tre rotazioni elementari sarà quello mostrato nella figura seguente.

Ogni rotazione elementare può essere trascritta come una matrice 3×3 (trasformazione omogenea).

Rotazione sull’asse X

$R{x} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & \cos\theta & -\sin\theta \\ 0 & \sin\theta & \cos\theta \end{pmatrix}$

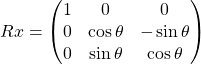
Rotazione sull’asse Y

$R{y} = \begin{pmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \end{pmatrix}$

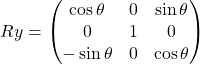
Rotazione sull’asse Z

$R{z} = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix}$

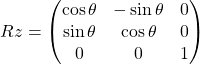
Python

In Python per esprimere le matrici esiste l’oggetto matrix della libreria numPy.

Infatti si può essere tentati di utilizzare il più comune np.array. Ma anche se le dichiarazioni degli oggetti np.array da np.matrix risultano molto simili, il loro comportamento può risultare assai diverso in molti contesti.

Ecco le tre rotazioni elementari:

import numpy as np
import math as m

def Rx(theta):
  return np.matrix([[ 1, 0           , 0           ],
                   [ 0, m.cos(theta),-m.sin(theta)],
                   [ 0, m.sin(theta), m.cos(theta)]])

def Ry(theta):
  return np.matrix([[ m.cos(theta), 0, m.sin(theta)],
                   [ 0           , 1, 0           ],
                   [-m.sin(theta), 0, m.cos(theta)]])

def Rz(theta):
  return np.matrix([[ m.cos(theta), -m.sin(theta), 0 ],
                   [ m.sin(theta), m.cos(theta) , 0 ],
                   [ 0           , 0            , 1 ]])

Gli angoli di Eulero

Quindi una generica rotazione è descritta a sua volta da una matrice di rotazione R. Qualsiasi matrice di questo tipo può essere descritta come il prodotto di successive rotazioni inotrno ai principali assi delle coordinate XYZ, presi in un ordine preciso.

Quindi una qualsiasi rotazione potrebbe essere scomposta nella sequenza di tre matrici elementari. Per esempio, la più intuibile è quella che si ottiene dapprima effettuando una rotazione sull’asse X di un angolo φ , poi sull’asse Y di un angolo θ ed infine sull’asse Z di un angolo ψ

$R{x} (\varphi) \rightarrow R{y} (\theta) \rightarrow R{z} (\psi)$

La tripletta degli angoli utilizzati in queste rotazioni elementari sono gli angoli di Eulero e vengono indicati normalmente (φ,θ,ψ).

Facciamo un esempio in Python. Scegliamo tre angoli di eulero e poi eseguiamo la moltiplicazione delle matrici elementari di rotazione RZYZ

phi = m.pi/2
theta = m.pi/4
psi = m.pi/2
print("phi =", phi)
print("theta  =", theta)
print("psi =", psi)


R = Rz(psi) * Ry(theta) * Rx(phi)
print(np.round(R, decimals=2))

Eseguendo otterremo la seguente matrice di rotazione

[[ 0. -0. 1. ]
[ 0.71 0.71 -0. ]
[-0.71 0.71 0. ]]

Ma è possibile eseguire anche l’operazione inversa. Cioè conoscendo la matrice di rotazione è possibile ricavare i tre angoli di Eulero.

import sys
tol = sys.float_info.epsilon * 10

if abs(R.item(0,0))< tol and abs(R.item(1,0)) < tol:
   eul1 = 0
   eul2 = m.atan2(-R.item(2,0), R.item(0,0))
   eul3 = m.atan2(-R.item(1,2), R.item(1,1))
else:   
   eul1 = m.atan2(R.item(1,0),R.item(0,0))
   sp = m.sin(eul1)
   cp = m.cos(eul1)
   eul2 = m.atan2(-R.item(2,0),cp*R.item(0,0)+sp*R.item(1,0))
   eul3 = m.atan2(sp*R.item(0,2)-cp*R.item(1,2),cp*R.item(1,1)-sp*R.item(0,1))

print("phi =", eul1)
print("theta  =", eul2)
print("psi =", eul3)

Eseguendo ricaviamo i tre angoli, che poi sono gli stessi che avevamo inserito all’inizio.

phi = 1.5707963267948966
theta = 0.7853981633974483
psi = 1.5707963267948966

Ma la sequenza di rotazione XYZ è solo una delle 12 possibili combinazioni. esistono diverse possibili combinazioni di tre rotazioni elementari, come ZYX, ZYZ, XYX, ecc.. Ognuna di queste avrà una diversa convenzione per esprimere gli angoli di Eulero.

La convenzione ZYZ

Oltre alla sequenza XYZ, un’altra molto comune è quella che fa riferimento alla convenzione associata agli angoli ZYZ caratterizzati dalle seguenti operazioni:

$R{z} (\varphi) \rightarrow R{y} (\theta) \rightarrow R{z} (\psi)$

Rotazione di un angolo φ intorno all’asse z
Rotazione di un angolo θ intorno all’asse y (corrente)
Rotazione di un angolo ψ intorno all’asse z (corrente)

L’ordine delle rotazioni elementari cambia il risultato finale.

Dove anche qui gli angoli φ, θ e ψ sono gli angoli di Eulero.

Per la convezione ZYZ, gli angoli di Eulero hanno una particolare nomenclatura:

φ è l’angolo di Precessione con valori [0, 2π]
θ è l’angolo di Nutazione
ψ è l’angolo di Rotazione propria

Ognuna delle tre rotazioni può essere rappresentata matematicamente mediante una matrice di rotazione. La matrice relativa alla rotazione complessiva viene calcolata moltiplicando le 3 matrici nell’ordine inverso.

Quindi, moltiplicando nell’ordine inverso otteniamo la matrice relativa alla rotazione complessiva:

$R{zyz} = R{z}R{y}R{z}$

Vediamo anche questo caso in Python. Reinseriamo gli stessi tre angoli di Eulero e moltiplichiamo le tre matrici elementari di rotazione nella giusta sequenza

phi = m.pi/2
theta = m.pi/4
psi = m.pi/2
print("phi =", phi)
print("theta  =", theta)
print("psi =", psi)


R = Rz(psi) * Ry(theta) * Rz(phi)
print(np.round(R, decimals=2))

Otterremo la seguente matrice di rotazione

[[-1. -0. 0. ]
[ 0. -0.71 0.71]
[-0. 0.71 0.71]]]

Anche qui è possibile eseguire l’operazione inversa. Cioè conoscendo la matrice di rotazione generale ricavare i tre angoli di Eulero. Dato che la condizione è diversa, anche le espressioni matematiche per ricaverli sono diverse.

eul1 = m.atan2(R.item(1,2),R.item(0,2))
sp = m.sin(eul1)
cp = m.cos(eul1)
eul2 = m.atan2(cp*R.item(0,2)+sp*R.item(1,2), R.item(2,2))
eul3 = m.atan2(-sp*R.item(0,0)+cp*R.item(1,0),-sp*R.item(0,1)+cp*R.item(1,1))

print("phi =", eul1)
print("theta =", eul2)
print("psi =", eul3)

Eseguendo il codice di sopra, ricaviamo i valori dei tre angoli di Eulero, che poi corrispondono proprio a quelli inseriti inizialmente.

phi = 1.5707963267948966
theta = 0.7853981633974483
psi = 1.5707963267948966

La rotazione di un punto nello spazio

Le trasformazioni di Eulero con i relativi angoli sono uno strumento meraviglioso per applicare delle rotazioni di punti nello spazio. L’esempio più semplice di applicazione di quello che abbiamo già visto nell’articolo è la rotazione di un punto situato in uno spazio di coordinate (X,Y,Z).

Un punto nello spazio può essere rappresentato mediante un vettore a 3 elementi che ne caratterizza i valori sui tre assi delle coordinate.

$v = \begin{bmatrix} x \\ y \\ z \end{bmatrix}$

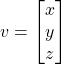
Quindi per il nostro esempio, partiremo da un punto semplice sull’asse X descritto dal seguente vettore.

$v = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$

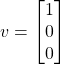
Che in Python si implementa

v1 = np.array([[1],[0],[0]])

Se vogliamo applicare una rotazione a questo punto sarà sufficiente moltiplicare questo vettore proprio con la matrice di rotazione ed ottenere così un altro vettore.

$v2 = R v1$

Che in Python si implementa nel modo seguente.

v2 = R * v1
print(np.round(v2, decimals=2))

Abbiamo aggiunto la funzione print() per visualizzare il risultato della rotazione. Le coordinate del punto nello spazio dopo la rotazione descritta da R corrisponderanno ai valori del vettore v2.

[[ 0. ]
[ 0.71]
[-0.71]]

Vediamo il risultato della nostra rotazione riportando su grafico con assi cartesiani la posizione del vettore (che descrive il punto) prima e dopo la rotazione.

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Cartesian axes
ax.quiver(-1, 0, 0, 3, 0, 0, color='#aaaaaa',linestyle='dashed')
ax.quiver(0, -1, 0, 0,3, 0, color='#aaaaaa',linestyle='dashed')
ax.quiver(0, 0, -1, 0, 0, 3, color='#aaaaaa',linestyle='dashed')
# Vector before rotation
ax.quiver(0, 0, 0, 1, 0, 0, color='b')
# Vector after rotation
ax.quiver(0, 0, 0, 0, 0.71, -0.71, color='r')
ax.set_xlim([-1.5, 1.5])
ax.set_ylim([-1.5, 1.5])
ax.set_zlim([-1.5, 1.5])
plt.show()

Eseguendo il codice si otterrà la rappresentazione grafica.

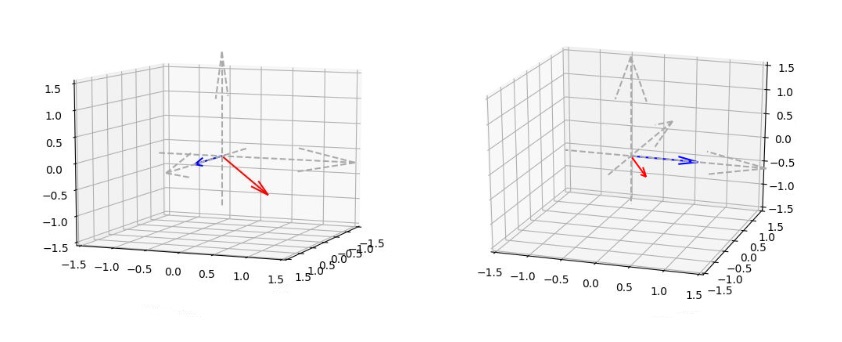
Angoli di Eulero - verso delle rotazioni elementari — Visualizzazione del vettore prima (blu) e dopo la rotazione (rosso)

Da qui poi si può passare alla rotazione di linee, figure geometriche e oggetti tridimensionali. Tutto alla base dei motori 3D con cui sono sviluppati moltissimi videogiochi.

Limiti della Rappresentazione di Eulero

Con questi esempi abbiamo visto come con gli angoli di Eulero sia possibile descrivere in maniera semplice qualsiasi rotazione nello spazio tridimensionale. Ma esiste una limitazione all’uso degli angoli di Eulero, a cui spesso ci si riferisce con il termine Gimbal Lock, in italiano Blocco Cardanico.

La tecnica che abbiamo visto si basa sull’utilizzo di una sequenza di rotazioni elementari riferendosi ad uno degli assi cartesiani alla volta. Applicando queste rotazioni in sequenza può succedere che uno degli assi di riferimento possa collassare in un altro. Per esempio con rotazioni di 90 gradi o di 180 gradi.

Ad esempio se ruotiamo di 90 gradi intorno all’asse X, l’asse Y collasserà sull’asse Z. In questa situazione si perde un grado di libertà in quanto le rotazioni intorno agli assi Y,Z diventano equivalenti.

Un altro inconveniente è che gli angoli dipendono dalla sequenza delle tre rotazioni intorno agli assi cartesiani e riportata come nome della convenzione: ZYZ, XZX, YXZ, ecc. Ognuna di queste sequenze dà una terna di angoli di Eulero con valori diversi, come abbiamo verificato anche sopra. Quindi di conseguenza cambierà anche la matrice di rotazione e la formula inversa.

Conclusioni

Nonostante tutti questi inconvenienti, gli angoli di Eulero sono oggi molto utilizzati e sono un punto di riferimento molto importante per chi lavora nel campo delle modellizzazioni CAD, dei motori 3D dei videogiochi, e della robotica e dell’automazione in generale. Tuttavia in pratica si ricorre spesso ad un modello matematico più complesso, ma più efficace, i quaternioni di Hamilton. In un prossimo articolo conosceremo come si implementano le rotazioni nello spazio con i quaternioni di Hamilton, cosa sono e come utilizzarli in Python.