Robot Dynamics

Post Views: 6.738

La dinamica in robotica, in inglese definita come robot dynamics, studia le forze che agiscono su un meccanismo robotico e le accelerazioni che queste forze producono. Generalmente si considera il meccanismo robotico come un sistema rigido, in modo da applicare le leggi dinamiche dei corpi rigidi.

Robot Dynamics - La dinamica in robotica

Introduzione alla Robot dynamics

Quando si ha a che fare con un meccanismo robotico, come per esempio un robot manipolatore, si deve tenere conto della sua funzionalità di base: il suo corretto posizionamento. Quando questo deve muoversi da una posizione di partenza ad una di arrivo, dovremo conoscere tutte le proprietà dinamiche del manipolatore, in modo da prevedere come le varie forze ed accelerazioni influiranno sul movimento.

Se per esempio, per produrre il movimento verranno applicate forze troppo piccole, potremo avere un movimento troppo lento, mentre se saranno troppo forti, rischieremo di far urtare il manipolatore con altri oggetti presenti nell’ambiente, oscillando eccessivamente rispetto alla posizione desiderata.

E’ per questo motivo che si sono definite delle equazioni dinamiche del moto in robotica. Ma la loro derivazione non è certamente un’operazione molto semplice da fare. In particolare la complessità aumenta con il crescere del numero di gradi di libertà del sistema robotico, e le molte non linearità presenti in tali sistemi.

Per tale scopo ci vengono in aiuto quindi delle tecniche basate sulla dinamica Lagrangiana. Queste tecniche ci permettono di ricavare in modo sistematico le equazioni del moto dei sistemi robotici.

Le due principali problematiche nella dinamica robotica sono:

Forward dynamics: date le forze, si ricavano le accelerazioni
Inverse dynamics: date le accelerazioni si ricavano le forze

La Forward dynamics è nota anche come dinamica diretta, o semplicemente dinamica. Viene utilizzata principalmente per la simulazione.

La Inverse dynamics, o dinamica inversa, viene invece utilizzata per il controllo diretto sul moto e le forze coinvolte di un meccanismo robotico, o anche per lo studio della traiettoria, per l’ottimizzazione, per la progettazione dei meccanismi robotici.

Altre problematiche che concernono la robot dynamics sono:

Calcolo dei coefficienti nell’equazione del moto
Identificazione dei parametri inerziali
Hybrid dynamics: date alcune forze e alcune accelerazioni, si ricavano le forze e le accelerazioni mancanti.

Equazioni del moto

Le equazioni del moto per un sistema fisico descrivono il suo moto come una funzione del tempo e di parametri opzionali di controllo in ingresso (control inputs). Nella forma generale le equazioni del moto assumono la seguente forma generalizzata.

$F (q(t), \dot{q}(t), \ddot{q}(t), u(t), t) = 0$

dove

t è la variabile tempo,
q è il vettore delle coordinate generalizzate, per esempio il vettore degli angoli dei giunti di un manipolatore
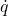$\dot{q}$ è il vettore delle velocità (derivata prima di q)
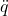$\ddot{q}$ è il vettore delle accelerazioni (derviata seconda di q)
u è il vettore dei parametri di controllo in ingresso

Le equazioni del moto permettono di ottenere una mappatura tra lo spazio di controllo e i comandi inviati agli attuatori, e tra lo spazio degli stati ed il movimento del robot.

In robotica si introducono delle assunzioni:

Corpi rigidi: in robotica, tutti i sistemi, come per esempio i manipolatori, si considerano costituiti da un insieme di parti rigide (link) collegate tra di loro da dei giunti regolati da un motore (actuated joints). Questa assunzione ci permette di utilizzare la teoria della dinamica dei corpi rigidi.
Il principio di D’Alembert: le forze interne (constraint forces) sono conservative. Queste forze agiscono su ciascun giunto in modo da impedire qualsiasi movimento al di fuori degli assi di giunto.

Le equazioni del moto per i Manipolatori

I manipolatori sono un caso particolare dei sistemi articolati dove almeno uno dei link è fissato all’ambiente. Le equazioni del moto per un manipolatore si possono scrivere nel seguente modo:

$M(q) \ddot{q} + \dot{q}^T C(q) \dot{q} = \tau + \tau_g (q)$

dove i gradi di libertà del robot si possono scrivere:

$n=dim(q)$

e dove

M(q) è la matrice n×n di inerzia,
C(q) è il tensore n×n×n di Coriolis,
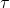$\tau$ è il vettore n-dimensionale delle torsioni dei giunti azionati (actuated joint)
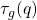$\tau_g(q)$ è il vettore n-dimensionale delle torsioni dei giunti esterni causate dalla gravità

Robot dynamics - angoli del robot manipolatore

Contrariamente alla forma generale $F (q(t), \dot{q}(t), \ddot{q}(t), u(t), t) = 0$ , questa espressione è invariante nel tempo, infatti t non appare nella formula. In questo modo, conoscendo lo stato corrente $(q,\dot{q})$ e la torsione applicata al giunto $\tau$ , si può calcolare direttamente le accelerazioni risultanti ai giunti $\ddot{q}$ . Questa operazione è nota come forward dynamics, cioè dinamica diretta.

Il sistema quindi non ha memoria. Indipendentemente da come si è giunti ad un particolare stato, partendo da quello stato si avrà sempre un’accelerazione uguale.

La matrice di inerzia M e il tensore di Coriolis

La matrice di inerzia M ed il tensore di Coriolis possono essere derivati dall’inerzia dei link e dal loro Jacobiano:

$M(q) = \sum_i J_i^t(q)^T m_i J_i^t (q) + J_i^R(q)^T I_i J_i^R(q)$

$\dot{q}^T C(q) = \sum_i J_i^t(q)^T m_i \dot{J}_i^t (q) + J_i^R(q)^T I_i \dot{J}_i^R(q) - J_i^R (q)^T( I_i J_i^R \dot{q}) \times J_i^R$

dove mi è la massa totale del link i, Ii è la sua matrice di inerzia, e Ji è il Jacobiano del frame attaccato al link i.

Il Jacobiano rotazionale 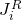$J_i^R$ è tale che la velocità angolare ωi del frame deli link rispetto al frame inerziale soddisfi $\omega_i = J_i^R \dot{q}$
il Jacobiano traslazionale 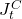$J_t^C$ è tale che la velocità lineare 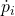$\dot{p}_i$ dell’origine del frame del link inerziale soddisfi $\dot{p}_i=J_i^t \dot{q}$ .

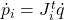Torsione di gravità e forze esterne

Le forze esterne applicate al sistema possono essere espresse attraverso una formula simile:

$\tau_{ext} (q) = \sum_i J_i^t (q)^T f_{ext,i} + J_i^R (q)^T \tau_{ext,i}$

dove fext,i denota la risultante delle forze esterne applicata al link i del robot e τext,i è il momento di queste forze. Insieme formano il la chiave inglese esterna applicata al link. Le coordinate della chiave inglese dovrebbe essere consistenti con la definizione delle nostre matrici Jacobiane. Assumendo che l’immagine delle nostre matrici Jacobiane sono espresse nel frame inerziale, allora le coordinate della chiave inglese dovrebbero essere espresse nel frame iniziale allo stesso modo.

Consideriamo la gravità come la nostra forza esterna. Assumendo che il frame attaccato al link i sia localizzata nel centro della massa del link, le torsioni del giunto causate dalla gravità si possono esprimere:

$\tau_g(q) = \sum_i m_i J_i^t (q)^T g$

Per definizione, il Jacobiano Jcom del centro di massa è tale che

$\sum_i m_i J_{com} = \sum_i m_i J_i^t$

e quindi l’espressione precedente si può cambiare in:

$\tau_g (q) = m J_{com} (q) g$

Modelli dinamici

Le equazioni del moto dipendono dal modello dinamico (dynamic model) corrispondente al meccanismo robotico in studio. Il modello dinamico non è altro che una descrizione del meccaniscmo robotico in termini delle parti che lo compongono: link, joints e dei parametri che caratterizzano queste componenti.

In particolare un modello dinamico consiste:

un modello cinematico del meccanismo robotico
un insieme di parametri inerziali

Sono richiesti 10 parametri inerziali per definire l’inerzia di un singolo corpo rigido (massa, posizione del centro di massa, e 6 parametri inerziali di rotazione). Quindi ogni modello dinamico avrà ben 10 parametri inerziali per ogni componente (corpo rigido individuabile) del meccanismo robotico.

Comunque, quando i corpi sono connessi tra di loro per formare un meccanismo robotico, come per esempio un manipolatore, si eliminano alcuni gradi di libertà del sistema. Infatti alcuni di essi non avranno più effetto sul comportamento dinamico del sistema.

La procedura di base, una volta identificato un modello cinematico ed effettuata una serie di misure del suo comportamento dinamico, sarà quindi quella di identificare i valori di un insieme di parametri inerziali di base che sono poi quelli osservabili sperimentalmente.

Esistono diverse metodologie su cui, dato un meccanismo robotico, si può derivare un modello dinamico. Tuttavia i pià noti sono:

metodo Lagrangiano
metodo di Newton-Eulero

Il metodo Lagrangiano è più semplice e sistematico, mentre il secondo è più efficiente soprattutto dal punto di vista del calcolo computazionale.

Metodo Lagrangiano

Il metodo di Lagrange si basa sul calcolo di una determinato valore, chiamato Lagrangiana, che è proprio del sistema meccanico da cui derivare il modello. Quello di Lagrange è un approccio energetico che permette di derivare le equazioni della dinamica in forma simbolica (o forma chiusa), cioè non numerica, facilitando così lo studio delle proprietà e l’analisi degli schemi di controllo.

La Lagrangiana è pari alla differenza tra l’energia cinetica T e l’energia potenziale U del sistema:

$L = T – U$

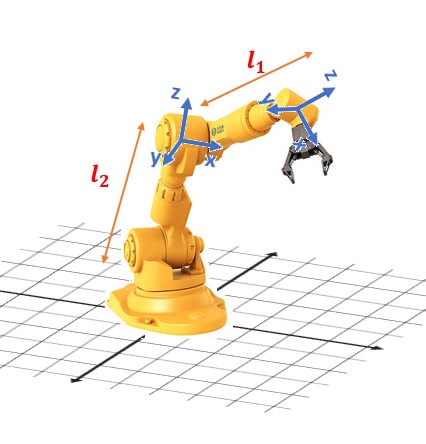
Questo particolare valore dipende sia da parametri dinamici (masse e momenti di inerzia dei link) sia da parametri geometrici (lunghezza dei link).

Si può dimostrare che esistono le seguenti equazioni di Lagrange

$\frac {d} {dt} \frac {\partial L} {\partial \dot{q}_i} - \frac {\partial L} {\partial q_i} = \xi_i , i = 1, ... , n$

Dove con $\xi_i$ si indicano le forze generalizzate associate alle coordinate generalizzate $q_i$ .

La particolarità di questo metodo è che la grandezza lagrangiana è espressa in forma simbolica e può essere manipolata ed elaborata attraverso un approccio sistematico. Una volta ottenuta quindi l’espressione della Lagrangiana, si può derivare il modello dinamico corrispondente, grazie ad una serie di equazioni, chiamate di equazioni di Eulero-Lagrange, direttamente ricavabili da essa.

Per esempio per un manipolatore robotico l’energia cinetica è data da:

$T(q, \dot{q}) = \frac{1}{2} \dot{q}^T B(q)\dot{q}$

Dove B è la matrice di Inerzia. Mentre l’eneriga potenziale è data da:

$U(q) = \sum_{i=1}^{n} - m_i g^T p_{C_i}$

Da cui si ottiene l’equazione Lagrangiana:

$L(q, \dot{q} ) = T(q, \dot{q}) - U(q) = \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} b_{ij} (q) \dot{q}_i \dot{q}_j + \sum_{i=1}^{n} m_i q^T p_{C_i}$

Derivando e apponendo le opportune operazioni si arriva alla forma matriciale:

$B(q) \ddot{q} + C (q, \dot{q}) \dot{q} + g(q) = \tau$

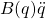$B(q) \ddot{q}$ Termini inerziali
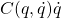$C (q, \dot{q}) \dot{q}$ Termini centrifughi e di Coriolis
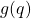$g(q)$ Termini gravitazionali
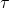$\tau$ Coppie ai giunti

Dove $\dot{q}$ e $\ddot{q}$ sono le velocità e le accelerazioni dei giunti, $B (q)$ è la matrice inerziale del manipolatore, $C (q, \dot{q}) \dot{q}$ è un termine in velocità che descrive gli effetti centrifughi e di Coriolis, mentre $g (q)$ è un termine gravitazionale dipendente solo dalla configurazione. Infine $\tau$ descrive l’effetto di eventuali forze e momenti esercitati dall’ambiente esterno sul robot.

Il modello dinamico del manipolatore, così come mostrato nell’equazione precedente, è stato formulato nello spazio dei giunti. Ciò nonostante è possibile ricavarne una formulazione anche nello spazio operativo.

E’ importante notare infine che nella derivazione del modello dinamico non si è tenuto conto del sistema di attuazione, costituito da motori e sistema di trasmissione. Il sistema di attuazione contribuisce agli effetti dinamici in vari modi: cambiando ad esempio i parametri di inerzie e masse dei link, e introducendo dinamiche proprie (elettromeccaniche) e possibili effetti non lineari come giochi, attriti ed elasticità. Tutti questi effetti possono comunque essere considerati introducendo opportune modifiche al modello dinamico. Sul manipolatore possono inoltre agire coppie di attrito viscoso e coppie di attrito statico.

Esistono metodi sistematici per ricavare i coefficienti della matrice d’inerzia e
quindi, per derivazione, quelli centrifughi e di Coriolis. Tuttavia la scrittura del modello dinamico basata sulle equazioni di Lagrange, pur dando luogo ad un modello in forma chiusa, facilmente interpretabile ed utilizzabile nella sintesi del controllore, costituisce un procedimento inefficiente dal punto di vista computazionale.

Metodo di Newton-Eulero

Una strada alternativa per la formulazione del modello dinamico è quella che va sotto il nome di metodo di Newton-Eulero.

Questo metodo si basa sull’utilizzo di due equazioni: l’equazione dinamica di Newton, secondo cui la somma delle forze agenti su un sistema meccanico è pari alla variazione della quantità di moto, e l’equazione dinamica di Eulero, secondo cui la somma dei momenti è pari alla variazione del momento della quantità di moto.

Il metodo di Newton-Eulero consiste quindi nello scrivere i bilanci di forze (equazioni di Newton) e di momenti (equazioni di Eulero) agenti su ciasun link, mettendo in evidenza le interazioni con i link contigui nella catena cinematica. In questo modo si ottiene un sistema di equazioni che possono essere risolte in modo ricorsivo, propagando le velocità e le accelerazioni dalla base verso l’organo terminale, e le forze e i momenti in senso opposto.

Si ottiene un sistema di equazioni che possono essere risolte in modo ricorsivo, propagando le velocità ed accelerazioni dalla base verso l’organo terminale, e le forze ed i momenti in senso opposto. La ricorsività rende l’algoritmo di Newton-Eulero computazionalmente efficiente.

Queste formule ricorsive possono essere valutate sia in modo simbolico che numerico, tuttavia è solo nella seconda modalità, quella numerica, che la ricorsività rende l’algoritmo di Newton-Eulero particolarmente efficiente da un punto di vista computazionale.

Lagrange vs. Newton-Eulero

Nonostante l’approccio Lagrangiano e quello di Newton-Eulero, risolto in forma simbolica, producano alla fine lo stesso modello matematico per la dinamica di un manipolatore, è possibile evidenziare alcune differenze tra queste due formulazioni.

Formulazione di Lagrange:

è sistematica e facilmente comprensibile
fornisce le equazioni del moto in forma analitica compatta, mettendo in  evidenza la matrice di inerzia, i termini centrifughi e di Coriolis, ed i termini gravitazionali. Questi elementi sono utili ai fini del progetto di un controllore basato sul modello.
si presta all’introduzione nel modello di effetti dinamici più complessi (deformabilità ai giunti o nei link)

Formulazione di Newton-Eulero:

è un metodo ricorsivo, efficiente dal punto di vista computazionale
è raccomandato per l’uso in tempo reale

Algoritmi in Robot dynamics

Dal punto di vista pratico, al momento attuale si utilizzano principalmente 3 diversi algoritmi nella robot dynamics:

Recursive Newton-Euler algorithm (RNEA). Questo algoritmo risolve i problemi di inverse dynamics, ed ha una complessità computazione di O(n). Può essere utilizzato per calcolare C nell’equazione del moto.
Articulated-body algorithm (ABA). Questo algoritmo risolve i problemi di forward dynamics, e ha una complessità computazionale di O(n).
Composite-rigid-body algorithm (CRBA). Questo algoritmo calcola la matrice inerziale dello spazio dei giunti, M , e ha una complessità computazionale di O(n2).

L’approfondimento sulle funzionalità di questi algoritmi e sulle loro specifiche verranno trattati in altri articoli.

References

Robot Dynamics from Scholarpedia
Equations of motion from Scaron.info

Robot Dynamics – La dinamica in Robotica